1. Восемь футбольных команд провели турнир в один круг (каждая сыграла с каждой по одному разу). Какое наименьшее число очков гарантирует команде место в четверке лидеров? В современном футболе за победу дают 3 очка, за ничью - 1, за поражение - 0.
2. Существуют ли 100 таких различных натуральных чисел, что квадрат каждого из них делится на сумму остальных?
3. Натуральные числа от 1 до 127 разбили на несколько (больше, чем на одну) групп с равными суммами. Докажите, что количество этих групп четно.
4. В равнобедренном прямоугольном треугольнике АВС (АВ=ВС) провели медианы AD и СЕ. Медиану AD продолжили на ее длину за точку D. Получилась точка Х. Медиану СЕ продолжили на ее длину за точку С. Получилась точка Y. Докажите, что угол AXY - прямой.
5. На kn карточках с двух сторон написаны числа от 1 до n по 2k раз каждое. Докажите, что эти карточки можно положить на стол так, чтобы сверху каждое число было написано ровно k раз.
6. Решите в простых числах уравнение p2 + q = 37q2 + p.
7. На клетчатой бумаге отметили 36 вершин клеток так, что они образовали квадрат 5*5. За один ход разрешается провести отрезок длины 2. Какое наименьшее число ходов надо сделать, чтобы от любой отмеченной вершины до любой другой можно было добраться по проведенным отрезкам, если переходить с одного отрезка на другой можно только в отмеченных точках?
8. В языке привидений всего две буквы: Ы и У. Два слова означают одно и то же, если одно получается из другого при помощи некоторого числа следующих операций: вычёркивание (соответственно вставка) десяти одинаковых букв, идущих подряд, замена набора стоящих рядом букв УЫ набором ЫУУ или наоборот. Докажите, что среди любых 200 слов языка привидений найдутся два, означающие одно и то же.
1. Восемь футбольных команд провели турнир в один круг (каждая сыграла с каждой по одному разу). Какое наименьшее число очков гарантирует команде место в четверке лидеров? В современном футболе за победу дают 3 очка, за ничью - 1, за поражение - 0.
2. Существуют ли 100 таких различных натуральных чисел, что квадрат каждого из них делится на сумму всех чисел?
3. Натуральные числа от 1 до 127 разбили на несколько (больше, чем на одну) групп с равными суммами. Докажите, что количество этих групп четно.
4. Решите в простых числах уравнение p2 + q = 5q2 + p.
5. На kn карточках с двух сторон написаны числа от 1 до n по 2k раз каждое. Докажите, что эти карточки можно положить на стол так, чтобы сверху каждое число было написано ровно k раз.
6. В матбое участвовали три команды. Перед боем игрок Иванов перешел из первой команды во вторую, игрок Петров - из второй команды в третью, а игрок Сидоров - из третьей команды в первую. После этого средний возраст первой команды увеличился на неделю, второй - увеличился на две недели, а третьей - уменьшился на 4 недели. Известно, что в первой и второй командах по 12 игроков. Сколько игроков в третьей команде?
7. В треугольнике АВС выполнены соотношения АВ=1, ВС=2, /АВС = 120o. Докажите, что медиана BD перпендикулярна стороне АВ.
8. В языке привидений всего две буквы: Ы и У. Два слова означают одно и то же, если одно получается из другого при помощи некоторого числа следующих операций: вычёркивание (соответственно вставка) десяти одинаковых букв, идущих подряд, замена набора стоящих рядом букв УЫ набором ЫУУ или наоборот. Докажите, что среди любого 101 слова языка привидений найдутся два, означающие одно и то же.
1. Восемь футбольных команд провели турнир в один круг (каждая сыграла с каждой по одному разу). Какое наименьшее число очков гарантирует команде место в четверке лидеров? В современном футболе за победу дают 3 очка, за ничью - 1, за поражение - 0.
2. Существуют ли 100 таких различных натуральных чисел, что квадрат каждого из них делится на сумму всех чисел?
3. Натуральные числа от 1 до 127 разбили на несколько (больше, чем на одну) групп с равными суммами. Докажите, что этих групп - четное число.
4. В матбое участвовали три команды. Перед боем игрок Иванов перешел из первой команды во вторую, игрок Петров - из второй команды в третью, а игрок Сидоров - из третьей команды в первую. После этого средний возраст первой команды увеличился на неделю, второй - увеличился на две недели, а третьей - уменьшился на 4 недели. Известно, что в первой и второй командах по 12 игроков. Сколько игроков в третьей команде? (199)
5. На kn карточках с двух сторон написаны числа от 1 до n по 2k раз каждое. Докажите, что эти карточки можно положить на стол так, чтобы сверху каждое число было написано ровно k раз.
6. В стране 201 город, из каждого выходит ровно 10 дорог, причем из любого города можно доехать до любого другого. Докажите, что можно выбрать 20 городов, никакие два из которых не соединены дорогой.
7. Решите в простых числах уравнение p2 + q = 5q2 + p.
8. В языке привидений всего две буквы: Ы и У. Два слова означают одно и то же, если одно получается из другого при помощи некоторого числа следующих операций: вычёркивание (соответственно вставка) десяти одинаковых букв, идущих подряд, замена набора стоящих рядом букв УЫ набором ЫУУ или наоборот. Докажите, что среди любого 101 слова языка привидений найдутся два, означающие одно и то же.
1. Для каких n числа от 1 до n можно записать в строчку в таком порядке, чтобы для любого k от 1 до n сумма первых k чисел строки делилась на k?
2. Петя, Вася и Толя решили сыграть в следующую игру. В кучке лежат 1999 спичек. Петя и Вася имеют право брать 1 или 2 спички, а Толя -1, 2 или 3. При этом Петя и Вася объединяют свои усилия против Толи, а Толя имеет право выбрать очередь своего хода - первый, второй или третий. Выигрывает тот, кто возьмет последнюю спичку. Может ли Толя выбрать себе такую очередь, что при правильной игре выиграет именно он?
3. Какое наибольшее число ладей можно расставить на шахматной доске 8*8 так, чтобы каждая ладья била нечетное число ладей? (53)
4. Равнобедренный прямоугольный треугольник AMN (AM = MN) расположен в квадрате ABCD так, что точка М лежит внутри квадрата, а точка N - на стороне CD. Докажите, что точка M лежит на диагонали BD.
5. После вечера танцев, где юноши танцевали с девушками, всех его участников спросили, со сколькими партнерами (партнершами) они танцевали. Были получены следующие ответы: 3, 3, 3, 3, 3, 5, 6, 6, 6. Докажите, что кто-то ошибся.
6. Клетки кубика Рубика раскрашены в черный и белый цвета так, что в любом прямоугольнике 1*4 одно и то же количество черных клеток. Докажите, что кубик либо весь черный, либо весь белый.
7. При каком наименьшем натуральном n в квадрате 5*5 можно расставить 25 различных натуральных чисел, не превосходящих n, так чтобы любые два соседних (находящихся в клетках, имеющих общую сторону или вершину) числа были взаимно просты?
8. Положительные числа a, b и c таковы, что a > b > c и a+b+c < 1. Докажите, что a2 + 3b2 + 5c2 < 1.
1. Можно ли записать в строку числа от 1 до 29 в таком порядке, чтобы для любого k от 1 до 29 сумма первых k чисел строки делилась на k?
2. В треугольнике ABC серединный перпендикуляр к стороне BC пересекает сторону AB в точке D и продолжение стороны AC в точке E. Докажите, что AD<AE.
3. После вечера танцев, где юноши танцевали с девушками, всех его участников спросили, со сколькими партнерами (партнершами) они танцевали. Были получены следующие ответы: 3, 3, 3, 3, 3, 5, 6, 6, 6. Докажите, что кто-то ошибся.
4. Клетки кубика Рубика раскрашены в черный и белый цвета так, что в любом прямоугольнике 1*4 одно и то же количество черных клеток. Докажите, что кубик либо весь черный, либо весь белый.
5. Сначала на доске написаны числа 1, 2, ..., 10. За один ход разрешается увеличить любое число на доске на сумму цифр любого из выписанных (в том числе на сумму цифр его самого). Можно ли добиться, чтобы каждое число превратилось в 9999?
6. Прямоугольник 1*9 прямолинейными разрезами рассекли на несколько частей, из которых удалось сложить квадрат (использовав все полученные части). Сколько, самое меньшее, могло быть частей?
7. При каком наименьшем натуральном n в квадрате 5*5 можно расставить 25 различных натуральных чисел, не превосходящих n, так чтобы любые два соседних (находящихся в клетках, имеющих общую сторону или вершину) числа были взаимно просты?
8. Петя, Вася и Толя решили сыграть в следующую игру. В кучке лежат 1999 спичек. Петя и Вася имеют право брать 1 или 2 спички, а Толя - 1, 2 или 3. При этом Петя и Вася объединяют свои усилия против Толи, а Толя имеет право выбрать очередь своего хода - первый, второй или третий. Выигрывает тот, кто возьмет последнюю спичку. Может ли Толя выбрать себе такую очередь, что при правильной игре выиграет именно он?
1. Можно ли записать в строку цифры от 1 до 9 в таком порядке, чтобы для любого k от 1 до 9 сумма первых k цифр в строке делилась на k?
2. Клетки квадрата 10*10 раскрашены в черный и белый цвета так, что в любом прямоугольнике 1*3 одно и то же количество черных клеток. Кроме того, в любом квадрате 2*2 также одно и то же количество черных клеток. Докажите, что все клетки квадрата 10*10 одинакового цвета.
3. Выписаны числа 1, 2,...,39, 40. Какое из чисел можно вычеркнуть, чтобы одно из оставшихся равнялось среднему арифметическому остальных? (Приведите все возможные варианты ответа.)
4. Разрежьте прямоугольник 1*5 на 5 частей, из которых можно сложить квадрат.
5. Сначала на доске написаны числа 1, 2, ..., 10. За один ход разрешается увеличить любое число на доске на сумму цифр любого из выписанных (в том числе на сумму цифр его самого). Можно ли добиться, чтобы каждое число превратилось в 9999?
6. После вечера танцев, где юноши танцевали с девушками, всех его участников спросили, со сколькими партнерами (партнершами) они танцевали. Были получены следующие ответы: 3, 3, 3, 3, 3, 5, 6, 6, 6. Докажите, что кто-то ошибся.
7. При каком наименьшем натуральном n в квадрате 4*4 можно расставить 16 различных натуральных чисел, не превосходящих n, так чтобы любые два соседних (находящихся в клетках, имеющих общую сторону или вершину) числа были взаимно просты?
8. Петя, Вася и Толя решили сыграть в следующую игру. В кучке лежат 1999 спичек. Петя и Вася имеют право брать 1 или 2 спички, а Толя - 1, 2 или 3. При этом Петя и Вася объединяют свои усилия против Толи, а Толя имеет право выбрать очередь своего хода - первый, второй или третий. Выигрывает тот, кто возьмет последнюю спичку. Может ли Толя выбрать себе такую очередь, что при правильной игре выиграет именно он?
1. В волейбольном турнире в играх любой тройки команд каждая побеждала один раз. Какое наибольшее количество команд могло участвовать в этом турнире.
2. На складе хранилось 1000 кг яблок, в которых содержалось 99% воды. Через месяц в результате усушки в яблоках оказалось 96% воды. Сколько кг яблок осталось на складе?
3. В треугольнике АВС на стороне АВ выбрали точку М, на стороне ВС - точку К. О - точка пересечения отрезков АК и СМ. Известно, что ОК = ОМ и угол ОАС равен углу ОСА. Докажите, что треугольник АВС - равнобедренный.
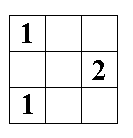
4. В клетках доски 3*3 стоят мины. Три клетки открыты, мин в них нет,
но написано количество мин стоящих в клетках доски, соседних по стороне или по
вершине с этой клеткой. Сколькими способами могут располагаться мины на этой
доске?

5. Дан выпуклый семиугольник. Сколько существует различных треугольников, сторонами которого являются его диагонали?
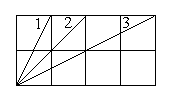
6. Найдите сумму углов 1,2,3 на рисунке справа.
7. Про положительные числа x, y, и z известно, что x+y=y+2z=z+3x. Какое из них самое большое?
1. У марсианских часов три стрелки. Первая стрелка обходит циферблат за полтора земных часа, вторая - за три, третья - за шесть. Первую стрелку поставили вертикально, вторую сместили на 120 градусов, а третью - на 240 градусов по часовой стрелке относительно первой. После этого часы запустили и стали считать, сколько раз встречаются две стрелки. Через сколько земных часов после запуска произойдет 1999-я такая встреча?
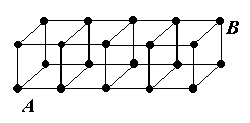
2. Дан решетчатый параллелепипед (см. рисунок), где длина каждого
отрезка равна 1 см. В точке А сидит таракан. Какое наибольшее
расстояние он может пройти по пути в точку В, не проходя ни через какую
точку дважды?
3. Сумма двух чисел равна сумме их квадратов. Докажите, что сумма этих чисел не больше 2.
4. Набор из нескольких натуральных чисел обладает таким свойством, что любое число, умноженное на сумму всех остальных, делится на сумму всех чисел. Докажите, что сумма квадратов этих чисел делится на сумму этих чисел.
5. На стороне AC равностороннего треугольника ABC с центром O выбрана точкаM. Точки N и K - основания перпендикуляров, опущенных из точки M на стороны AB и BC соответственно. Докажите, что прямая MO делит отрезок NK пополам.
6. В государстве 100 городов. Некоторые пары городов соединены дорогами, причем есть не менее четырех циклических маршрутов. Докажите, что есть циклический маршрут, проходящий не более, чем через 51 город.
7. Даны три отрезка длин 1, 2, 3. Отрезок длины 3 как-то разбили на 100 других. Докажите, что среди получившихся 102 отрезков найдутся три, из которых можно составить треугольник.
8. Можно ли натуральные числа от 1 до 1999 разбить на две группы так, чтобы произведение всех чисел одной группы равнялось сумме всех чисел второй группы?
1. У марсианских часов три стрелки. Первая стрелка обходит циферблат за полтора земных часа, вторая - за три, третья - за шесть. Первую стрелку поставили вертикально, вторую сместили на 120 градусов, а третью - на 240 градусов по часовой стрелке относительно первой. После этого часы запустили и стали считать, сколько раз встречаются две стрелки. Через сколько земных часов после запуска произойдет 600-я такая встреча?
2. Даны три отрезка длин 1, 2, 3. Отрезок длины 3 как-то разбили на 100 других. Докажите, что среди получившихся 102 отрезков найдутся три, из которых можно составить треугольник.
3. В государстве 90 городов. Некоторые пары городов соединены дорогами, причем есть не менее двух циклических маршрутов. Докажите, что есть циклический маршрут, проходящий не более, чем через 60 городов.
4. Квадратную таблицу размером 3*3 заполнили цифрами от 1 до 9, записав каждую ровно один раз. Может ли случиться, что для любой строки и любого столбца произведение трех стоящих в ней (нем) чисел делится на 4?
5. На стороне AC равностороннего треугольника ABC с центром O выбрана точка M. Точки N и K - основания перпендикуляров из точки M на стороны AB и BC соответственно. Докажите, что прямая MO делит отрезок NK пополам.
6. Сумма двух чисел равна сумме их квадратов. Докажите, что сумма этих чисел не больше 2.
7. Дан решетчатый параллелепипед (см. рисунок), где длина каждого
отрезка равна 1 см. В точке А сидит таракан. Какое наибольшее
расстояние он может пройти по пути в точку В, не проходя ни через какую
точку дважды?

8. Набор из нескольких натуральных чисел обладает таким свойством, что любое число, умноженное на сумму всех остальных, делится на сумму всех чисел. Докажите, что сумма квадратов этих чисел делится на сумму этих чисел.
1. У марсианских часов три стрелки. Первая стрелка обходит циферблат за полтора земных часа, вторая - за три, третья - за шесть. Первую стрелку поставили вертикально, вторую сместили на 120 градусов, а третью - на 240 градусов по часовой стрелке относительно первой. После этого часы запустили и стали считать, сколько раз встречаются две стрелки. Через сколько земных часов после запуска произойдет 600-я такая встреча?
2. Дан решетчатый параллелепипед (см. рисунок), где длина каждого
отрезка равна 1 см. В точке А сидит таракан. Какое наибольшее
расстояние он может пройти по пути в точку В, не проходя ни через какую
точку дважды?

3. Окружность длины 19 см катится без проскальзывания по неподвижной окружности длины 99 см. Один сантиметр неподвижной окружности измазали неистощимой краской: если что-то ею измажется, оно затем пачкает все, к чему прикасается. Движение подвижной окружности начинается с начала измазанного участка по направлению к нему. Какой путь подвижная окружность пройдет к моменту, когда неподвижная окружность впервые окажется измазанной полностью?
4. Квадратную таблицу размером 3*3 заполнили цифрами от 1 до 9, записав каждое ровно один раз. Может ли случиться, что для любой строки и любого столбца произведение трех стоящих в ней (нем) чисел делится на 4?
5. Даны семь положительных чисел: два из них равны 1 и 2, а сумма остальных пяти равна 3. Докажите, что среди этих семи чисел есть такие три, что сумма любых двух из них больше третьего.
6. В государстве 90 городов. Некоторые пары городов соединены дорогами, причем есть не менее двух циклических маршрутов. Докажите, что есть циклический маршрут, проходящий не более, чем через 60 городов.
7. Докажите, что можно выбрать 100 различных натуральных чисел так, чтобы каждое из них делило нацело сумму остальных.
8. Игра идет на клетчатой плоскости. Первый своим ходом рисует два непересекающихся отрезка единичной длины, идущие по линиям сетки, а второй достраивает один из только что нарисованных отрезков до квадрата так, чтобы он не имел общих точек с уже нарисованными фигурами. Проигрывает тот, кто не может сделать хода. Кто выигрывает при правильной игре?
1. На плоскости нарисованы три окружности так, как показано на
рисунке. Вначале в каждой из семи частей, на которые они делят плоскость,
стоит по единице. За один ход разрешается выбрать одну из окружностей и либо
сменить знаки всех стоящих внутри нее чисел, либо возвести все эти числа в
квадрат. Можно ли за несколько таких ходов добиться ситуации, когда в
центральной области стоит -1, а во всех остальных - единицы?
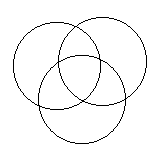
2. Обозначим через p(n) количество
простых чисел, не превосходящих n. Докажите, что
p(2n)+p(n!+n)>p(n)+p(n!+2n)
3. На планете 10000 городов, среди которых есть столицы государств. Некоторые города связаны дорогами так, что любая дорога соединяет ровно два города, и от любого города до любого другого можно добраться по дорогам. При этом, чтобы попасть из одной столицы в другую, нужно проехать не менее 200 дорог. Докажите, что на планете меньше 100 столиц.
4. На доске написаны числа 2, 3, 9. Разрешается заменить любые два числа а и b на числа a+b+(a2+b2)1/2 и a+b-(a2+b2)1/2 и Может ли на доске когда-нибудь появиться число, меньшее 1?
5. Верен ли признак равенства треугольников по двум высотам и медиане, проведенной к третьей стороне?
6. От картонного треугольника прямолинейными разрезами один за другим отрезают одинаковые треугольники. Найдется ли треугольник, для которого это удастся сделать хотя бы 13 раз?
7. На столе лежат 9 карточек, на которых написаны натуральные числа от 1 до 9. Двое по очереди берут карточки со стола. Побеждает тот, кто первым сумеет составить из своих карточек, знаков арифметических действий (+, -, *, : ) и скобок выражение, значение которого равно 40. Если по окончании игры такого выражения не может составить ни один из играющих, то считается, что игра закончилась вничью. Кто выиграет при правильной игре: тот, кто делает первый ход, или его партнер?
8. При каком наибольшем k существуют k подряд идущих натуральных чисел таких, что их суммы цифр являются перестановкой k подряд идущих натуральных чисел?
1. На плоскости нарисованы три окружности так, как показано на
рисунке. Вначале в каждой из семи частей, на которые они делят плоскость,
стоит по единице. За один ход разрешается выбрать одну из окружностей и либо
сменить знаки всех стоящих внутри нее чисел, либо возвести все эти числа в
квадрат. Можно ли за несколько таких ходов добиться ситуации, когда в
центральной области стоит -1, а во всех остальных - единицы?
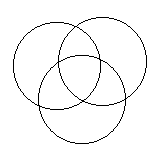
2. На планете 1000 городов, среди которых есть столицы государств. Некоторые города связаны дорогами так, что любая дорога соединяет ровно два города, и от любого города до любого другого можно добраться по дорогам. При этом, чтобы попасть из одной столицы в другую, нужно проехать не менее 21 дороги. Докажите, что на планете не больше 90 столиц.
3. Обозначим через p(n) количество
простых чисел, не превосходящих n. Докажите, что
p(2n)-p(n)>p(n!+2n)-p(n!+n)
4. Верен ли признак равенства треугольников по высоте и медиане, проведенным к одной стороне, и высоте, проведенной к другой стороне?
5. На столе лежат 9 карточек, на которых написаны натуральные числа от 1 до 9. Двое по очереди берут карточки со стола. Побеждает тот, кто первым сумеет составить из своих карточек, знаков арифметических действий (+, -, *, : ) и скобок выражение, значение которого равно 40. Если по окончании игры такого выражения не может составить ни один из играющих, то считается, что игра закончилась вничью. Кто выиграет при правильной игре: тот, кто делает первый ход, или его партнер?
6. Верно ли, что существует число, кратное 1999 и имеющее сумму цифр, равную 1999?
7. Можно ли замостить какую-нибудь бесконечную полосу клетчатой бумаги равнобедренными "уголками" из пяти клеток?
8. При каком наибольшем k существуют k подряд идущих натуральных чисел таких, что их суммы цифр являются перестановкой k подряд идущих натуральных чисел?
1. На плоскости нарисованы три окружности так, как показано на
рисунке. Вначале в каждой из семи частей, на которые они делят плоскость,
стоит по единице. За один ход разрешается выбрать одну из окружностей и либо
сменить знаки всех стоящих внутри нее чисел, либо возвести все эти числа в
квадрат. Можно ли за несколько таких ходов добиться ситуации, когда в
центральной области стоит -1, а во всех остальных - единицы?
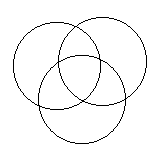
2. Обозначим через p(n) количество
простых чисел, не превосходящих n. Докажите, что
p(2n)+1>p(n!+2n)-p(n!)
3. На планете 1000 городов, среди которых есть столицы государств. Некоторые города связаны дорогами так, что любая дорога соединяет ровно два города, и от любого города до любого другого можно добраться по дорогам. При этом, чтобы попасть из одной столицы в другую, нужно проехать не менее 21 дороги. Докажите, что на планете не больше 90 столиц.
4. Цифры от 0 до 9 выписали в строчку так, что среди любых трех подряд идущих цифр сумма каких-то двух равна 7. Чему может быть равна сумма первой и последней цифр?
5. Обозначим через А сумму трех последовательных натуральных чисел, а через В - сумму трех следующих чисел. Может ли произведение АВ равняться 222222222222 (12 двоек)?
6. Как замостить какую-нибудь бесконечную полосу клетчатой бумаги равнобедренными "уголками" из пяти клеток?
7. На столе лежат 9 карточек, на которых написаны натуральные числа от 1 до 9. Двое по очереди берут карточки со стола. Побеждает тот, кто первым сумеет составить из своих карточек, знаков арифметических действий (+, -, *, : ) и скобок выражение, значение которого равно 14. Если по окончании игры такого выражения не может составить ни один из играющих, то считается, что игра закончилась вничью. Кто выиграет при правильной игре: тот, кто делает первый ход, или его партнер?
8. При каком наибольшем k существуют k подряд идущих натуральных чисел таких, что их суммы цифр являются перестановкой k подряд идущих натуральных чисел?