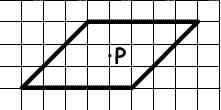
1. На рисунке изображен параллелограмм и отмечена точка P пересечения его диагоналей. Проведите через P прямую так, чтобы она разбила параллелограмм на две части, из которых можно сложить ромб.


2. Квадрат и прямоугольник одинакового периметра имеют общий угол. Докажите, что точка пересечения диагоналей прямоугольника лежит на диагонали квадрата.

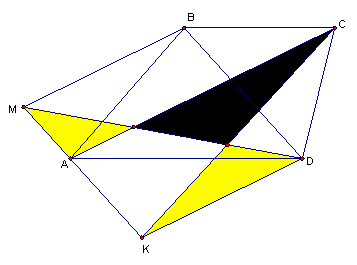
3. В треугольнике АВС АА₁ и ВВ₁ — высоты. На стороне АВ выбраны точки М и К так, что В₁К || BC и А₁М || АС. Д окажите, что угол АА₁К равен углу ВВ₁М.

4. Постройте треугольник по стороне, радиусу вписанной окружности и радиусу вневписанной окружности, касающейся этой стороны. (Исследование проводить не требуется.)

5. В некоторой точке круглого острова радиусом 1 км зарыт клад. На берегу острова стоит математик с прибором, который указывает направление на клад, когда расстояние до клада не превосходит 500 м. Кроме того, у математика есть карта острова, на которой он может фиксировать все свои перемещения, выполнять измерения и геометрические построения. Математик утверждает, что у него есть алгоритм, как добраться до клада, пройдя меньше 4 км. Может ли это быть правдой?

6. Фиксированы две окружности w₁ и w₂, одна их внешняя касательная l и одна их внутренняя касательная m. На прямой m выбирается точка X, а на прямой l строятся точки Y и Z так, что XY и XZ касаются w₁ и w2 соответственно, а треугольник XYZ содержит окружности w₁ и w₂. Докажите, что центры окружностей, вписанных в треугольники XYZ, лежат на одной прямой.

1. Существуют ли два таких четырехугольника, что стороны первого меньше соответствующих сторон второго, а соответствующие диагонали больше?

2. Трапеция ABCD и параллелограмм MBDK расположены так, что стороны параллелограмма параллельны диагоналям трапеции (см. рис.). Докажите, что площадь черной части равна сумме площадей желтых частей.


3. В остроугольном треугольнике АВС проведены высоты АА₁ и ВВ₁. Докажите, что перпендикуляр, опущенный из точки касания вписанной окружности со стороной ВС на прямую АС, проходит через центр вписанной окружности треугольника А₁СВ₁.

4. На медианах треугольника как на диаметрах построены три окружности. Известно, что они попарно пересекаются. Пусть C₁ — более удаленная от вершины C точка пересечения окружностей, построенных на медианах AM₁ и BM₂. Точки A₁ и B₁ определяются аналогично. Докажите, что прямые АА₁, ВВ₁ и СС₁ пересекаются в одной точке.

5. Докажите, что у любого выпуклого многогранника найдутся три ребра, из которых можно составить треугольник.

6. К двум окружностям w₁ и w₂, пересекающимся в точках А и В, проведена их общая касательная CD (C и D — точки касания соответственно, точка B ближе к прямой CD, чем А). Прямая, проходящая через А, вторично пересекает w₁ и w₂ в точках К и L соответственно (A лежит между K и L). Прямые KC и LD пересекаются в точке P. Докажите, что РВ — симедиана треугольника KPL (прямая, симметричная медиане относительно биссектрисы).