(В. Дольников, И. Богданов)
Заключительный этап
1999/2000 учебный год
Казань, 12-18 апреля 2000 г.
Задачи пятого (финального) этапа XXVI Российской олимпиады школьников по математике. Задания подготовлены Методическим Советом Российской математической олимпиады школьников.
9.1 Различные числа a, b и с таковы, что уравнения
x2+ax+1=0 и x2+bx+c=0 имеют общий действительный
корень. Кроме того, общий действительный корень имеют уравнения
x2+x+a=0 и x2+cx+b=0.
Найдите сумму a+b+c.
(Н. Агаханов)
9.2 Таня задумала натуральное число X<100, а Cаша пытается
его угадать. Он выбирает пару натуральных чисел M и N, меньших 100, и задаёт
вопрос: "Чему равен наибольший общий делитель X+M и N ?" Докажите, что Саша
может угадать танино число, задав 7 таких вопросов.
(А. Голованов)
9.3 Пусть O - центр описанной окружность w
остроугольного треугольника ABC. Окружность
w1 с центром K проходит через точки
A, O, C и пересекает стороны AB и BC в точках M и N. Известно, что точки
L и K симметричны относительно прямой NM. Докажите, что
BL | AC.
(М. Сонкин)
9.4 В стране несколько городов, некоторые пары городов соединены
дорогами. При этом из каждого города выходит хотя бы 3 дороги. Докажите,
что существует циклический маршрут, длина которого не делится на 3.
(Д. Карпов)
10.1 Найдите сумму
[1/3] + [2/3] + [22/3] + [23/2] + ... + [21000/3] .
10.2 Пусть -1<x1<x2<...<xn<1 и
(x1)13+(x2)13+...+(xn)13 = x1+x2+...+xn .
Докажите, что если y1<y2<...<yn, то(x1)13y1+(x2)13y2+...+(xn)13yn < x1y1+x2y2+...+xnyn .
10.3 В остроугольном неравнобедренном треугольнике ABC биссектриса
острого угла между высотами AA1 и CC1 пересекает стороны
AB и BC в точках P и Q соответственно. Биссектриса угла B пересекает отрезок,
соединяющий ортоцентр треугольника ABC с серединой стороны AC, в точке R.
Докажите что точки P, B, Q и R лежат на одной окружности.
(С. Берлов)
10.4 Имеются пять внешне одинаковых гирь с попарно различными массами.
Разрешается выбрать любые три из них A, B и C и спросить, верно ли, что
m(A)<m(B)<m(C). (Через m(x) обозначена масса гири x, при этом даётся
ответ "Да" или "Нет".) Можно ли за девять вопросов гарантировано узнать,
в каком порядке идут веса гирь?
(О. Подлипский)
11.1 Найдите все функции
f : R -> R, которые для всех
x, y, z C R удовлетворяют неравенству
f(x+y) + f(y+z) + f(z+x) > 3f(x+2y+3z)
11.2 Докажите, что можно разбить всё множество натуральных чисел на
100 непустых подмножеств так, чтобы в любой тройке a, b, c такой
что a+99b=c нашлись два числа из одного подмножества.
(Д. Джукич, Ф. Петров, И. Богданов, С. Берлов)
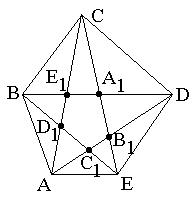
11.3 На координатной плоскости дан выпуклый пятиугольник ABCDE с
вершинами в целых точках. Докажите, что внутри или на границе пятиугольника
A1B1C1D1E1 (см. рис.)
есть хотя бы одна целая точка.

(В. Дольников, И. Богданов)
11.4 Дана последовательность неотрицательных целых чисел a1, a2, ..., an. Для любого k от 1 до n обозначим через mk величину
| ak-l+1 + ak-l+2 + ... + ak | |
| max | |
| l=1,2,...,k | l |
9.5 На доску последовательно выписываются числа a1=1,
a2, a3, ... по следующим правилам:
an+1=an-2, если число an-2 - натуральное
и ещё не выписано на доску, в противном случае an+1=an+3.
Докажите, что все квадраты натуральных чисел появятся в этой последовательности
при прибавлении 3 к предыдущему числу.
(Н. Агаханов)
9.6 В некоторых клетках доски 2n*2n стоят чёрные и белые фишки.
С доски сначала снимают все чёрные фишки, которые стоят в одной вертикали с
какой-либо белой, а затем все белые фишки, стоящие в одной горизонтали с
какой-либо из оставшихся чёрных. Докажите, что либо чёрныхЁ либо белых фишек
на доске осталось не более n2.
(С. Берлов)
9.7 На медиане CD треугольника ABC отмечена точка E. Окружность
S1, проходящая через E и касающаяся прямой AB в точке A, пересекает
сторону AC в точке M. Окружность S2, проходящая через Е и касающаяся
прямой AB в точке B, пересекает сторону BC в точке N. Докажите, что описанная
окружность треугольника CMN касается S1 и S2.
(М. Сонкин)
9.8 По окружности расставлено 100 натуральных чисел, взаимно простых
в совокупности. Разрешается прибавлять к любому числу наибольший общий делитель
его соседей. Докажите, что при помощи таких операций можно сделать все числа
попарно взаимно простыми.
(С. Берлов)
10.5 Пусть M - конечное множество чисел. Известно, что среди любых
трёх его элементов найдутся два, сумма которых принадлежит M. Какое наибольшее
число элементов может быть в M?
(Е. Черепанов)
10.6 Совершенное число, большее 6, делится на 3. Докажите, что оно
делится на 9. (Натуральное число называется совершенным, если оно
равно сумме всех своих делителей, отличных от самого числа, например 6=1+2+3.)
(А. Храбров)
10.7 Даны две окружности, касающиеся внутренним образом точки N.
Хорды BA и BC внешней окружности касаются внутренней в точках K и M
соответственно. Пусть Q и P - середины дуг AB и BC, не содержащих точку N.
Окружности, около треугольников BQK и BPM, пересекаются второй раз
в точке B1. Докажите, что BPB1Q - параллелограмм.
(Т. Емельянов)
10.8 На прямоугольном столе лежат равные картонные квадраты k
различных цветов со сторонами, параллельными сторонам стола. Если рассмотреть
любые k квадратов различных цветов, то какие-нибудь два из них можно прибить
к столу одним гвоздём. Докажите, что все квадраты некоторого цвета можно
прибить к столу 2k-2 гвоздями.
(В. Дольников)
11.5 Докажите неравенство
sinn(2x) + (sinnx - cosnx)2 < 1 .
11.6 Совершенное число, большее 28, делится на 7. Докажите, что оно
делится на 49. (Натуральное число называется совершенным, если оно
равно сумме всех своих делителей, отличных от самого числа, например 6=1+2+3.)
(А. Храбров)
11.7 Четырёхугольник ABCD описан около окружности
w. Продолжения сторон AB и CD пересекаются в точке O.
Окружность w1 касается стороны BC в точке
K и продолжений сторон AB и CD, окружность
w2 касается стороны AD в точке L и
продолжений сторон AB и CD. Известно, что точки O, K, L лежат на одной прямой.
Докажите, что середины сторон BC, AD и центр окружности
w лежат на одной прямой.
(П. Кожевников)
11.8 Клетки таблицы 100*100 окрашены в 4 цвета так, что в любой
строке и в любом столбце ровно по 25 клеток каждого цвета. Докажите, что
найдутся две строки и два столбца, все четыре клетки на пересечении которых
окрашены в разные цвета.
(С. Берлов)