Условия задач командной олимпиады

лига 8А		лига 9A		лига 10А		лига 11A
лига 8Б		лига 9Б (PDF)		лига 10Б		лига 11Б

Лига 8А

1. Игра.

   Играют двое на полоске из 101 клеточки, на концах которой стоит по одной шашке. Каждый может двигать свою шашку на одну, две или три клетки вперед или назад. Ходят по очереди, перепрыгивать через шашку противника нельзя. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

2. Квадрат.

   Постройте квадрат ABCD, если отмечены точки E, F, G, H такие, что E лежит на прямой AB, F √ на прямой BC, G √ на CD, H √ на DA, и известно, что решение единственное.

3. Сумма.

   В ряд стоят 7 неотрицательных чисел. Сумма любых трех чисел, стоящих подряд, равна 1. Какое наибольшее значение может быть у суммы всех семи чисел?

4. Углы.

   В четырехугольнике ABCD сумма углов ABD и BDC равняется 180^o, а стороны AD и BC равны. Докажите, что углы при вершинах A и C такого четырехугольника равны.

5. Целая часть

   Целая часть числа [x] √ это наибольшее целое число, не превосходящее x. Известно, что [a]=2000, а [b]=2. Какие значения может принимать [a∙b]?

6. Краски.

   На плоскости расположено 2007 точек, никакие три из которых не лежат на одной прямой. Все точки попарно соединены отрезками. Можно ли все отрезки раскрасить в 2006 цветов так, чтобы отрезки, выходящие из одной точки, были разного цвета?

7. Степени.

   Целые числа a, b, c таковы, что ab + bc + cd = 0. Докажите, что число abc можно представить в виде произведения квадрата целого числа на куб целого числа.

8. Доска.

   В каждой клетке доски 8x8 написано число так, что числа в соседних по стороне клетках отличаются ровно на 1. Известно, что в одной из клеток написано число 3, а в другой - 17. Докажите, что число 10 встречается в таблице ровно 8 раз.

Лига 8Б

1. На острове Рыцарей и Лжецов живут только рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. В Думе острова 11 депутатов. В целях сокращения бюджета было решено сократить Думу на одного депутата. Но каждый из депутатов заявил, что если его выведут из состава Думы, то среди оставшихся 10 депутатов большинство будет лжецами. Сколько рыцарей и лжецов в Думе?

2. Жюри, средний возраст которого 20 лет, состоит из 7 человек. Для судейства математических боев все жюри, кроме председателя, который появлялся то на одном бою, то на другом, разбилось на 3 бригады. При этом средний возраст членов жюри каждой бригады оказался равен 19 лет. Сколько лет председателю жюри?

3. Можно ли правильный треугольник со стороной 99 разрезать на трапеции, стороны каждой из которых равны 1, 1, 1, 2?

4. В 120-квартирном доме два 60-квартирных подъезда. Все жильцы купили новые номера квартир, при этом двузначные номера стояли вдвое, а трёхзначные - втрое дороже однозначных. Второй подъезд израсходовал 8460 рублей. Сколько рублей израсходовал первый подъезд?

5. Найдите значение выражения x² + y² + z², если x + y + z = 1 и .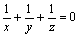

6. Найдите углы равнобедренного треугольника, у которого центры вписанной и описанной окружностей симметричны относительно основания.

7. Найти все пары натуральных чисел m и k, для которых k! + 12 = m². Здесь k! (читается "k факториал") - произведение всех натуральных чисел от 1 до k.

8. В вершинах квадрата расставили числа. Затем отметили каждое число, которое равно сумме трех чисел, соединенных с ним ребрами. Какое наибольшее число чисел может быть отмечено?

Лига 9А

1. В некоторой стране из любого города можно добраться в любой другой по дорогам (каждая дорога соединяет два города). В городах живут гонцы. Каждый год один из городов выпускает во все соседние города по одному гонцу (для этого в городе должно быть достаточно гонцов). Прошло несколько лет, и в каждом городе оказалось столько же гонцов, сколько было изначально. Какое наименьшее число гонцов может состоять на службе в этой стране, если в ней n городов и m дорог?

2. Вершины выпуклого четырёхугольника лежат внутри правильного треугольника со стороной 1. Докажите, что длина хотя бы одной из сторон четырёхугольника меньше 0,5.

3. Докажите, что для любых положительных чисел x₁>= x₂>= ...>= x_n>0 выполнено неравенство

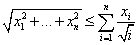
4. Дробная часть квадрата рационального числа r равна 1/4. Докажите, что число 2r - целое.

5. Какое наибольшее количество чисел можно выбрать из 1 , ..., 1000 так, чтобы сумма любых трёх различных выбранных чисел не была выбранным числом?

6. Пусть O - центр окружности w, описанной вокруг остроугольного треугольника ABC, W - середина той дуги BC окружности w, которая не содержит точку A и H - точка пересечения высот треугольника ABC. Найдите угол BAC, если WO=WH.

7. Решите уравнение (x+1)(x+2)(x+8)(x+9)=y² в целых числах.

8. Точки K и L - проекции вершин А и С остроугольного треугольника АВС на биссектрису внешнего угла при вершине В. Точки Н и М - основания высоты и медианы, проведённых из вершины В. Докажите, что точки H, M, K и L лежат на одной окружности.

Лига 10А

1. Верно ли, что для любого x>= 1 ?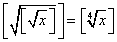

2. Дан треугольник ABC. Две прямые, симметричные прямой АС относительно прямых АВ и ВС соответственно, пересекаются в точке К. Докажите, что прямая ВК проходит через центр описанной окружности треугольника АВС.

3. Докажите, что при любом n число 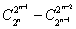делится на 4^n-1.

4. Имеется N человек, незнакомых между собой. Докажите, что при любом N их можно познакомить так, чтобы никакие трое не имели поровну знакомых.

5. Какое наибольшее число точек можно расположить на плоскости так, чтобы среди их попарных расстояний было бы только два различных?

6. Найдите все функции f(x), удовлетворяющие соотношению xf(y)+yf(x)=(x+y)f(x)f(y) при любых действительных x, y.

7. Пусть A,B,C - углы, a, b, c - стороны треугольника. Докажите неравенство .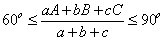

8. Существует ли квадрат, вершины которого лежат на четырех концентрических окружностях, радиусы которых образуют арифметическую прогрессию?

Лига 10Б

1. В клетках таблицы mxn расставлены числа так, что в каждой строке и каждом столбце числа образуют арифметическую прогрессию. Известно, что сумма чисел, стоящих в угловых клетках, равна S. Найти сумму всех чисел в таблице.

2. Найдите все нечётные натуральные n, для которых (n-1)! не делится на n².

3. Десять спортсменов участвовали в турнире по настольному теннису. Каждые два из них сыграли между собой ровно одну партию. Первый игрок одержал x₁ побед и потерпел y₁ поражений, второй одержал x₂ побед и потерпел y₂ поражений и т.д. Докажите, что x₁²+...+x₁₀²=y₁²+...+y₁₀².

4. На стороне AC треугольника ABC выбирается точка K, а на медиане BD - точка P так, что площадь треугольника APK равна площади треугольника BPC. Найти геометрическое место точек пересечения прямых AP и BK.

5. На острове, население которого составляют только рыцари, всегда говорящие правду и лжецы, которые всегда лгут, находится НИИ. Каждый из его сотрудников однажды сделал два заявления:
   а) В институте нет и десяти человек, которые работают больше меня;
   б) По крайней мере сто человек в институте получают зарплату большую, чем моя.
   Известно, что нагрузка у всех работников разная, как и зарплата. Сколько человек работает в НИИ?

6. Параллельно сторонам треугольника проведены три прямые. Каждая из прямых удалена от стороны, которой она параллельна, на расстояние, равное длине этой стороны. При этом для каждой стороны треугольника параллельная ей прямая и противолежашая этой стороне вершина расположены по разные стороны от неё. Докажите, что точки пересечения продолжений сторон треугольника с тремя проведёнными прямыми лежат на одной окружности.

7. Найдите все функции f(t) такие, что для любых x и y f(x-y)=f(x)+f(y)-2xy.

8. На листе бумаги нарисован правильный треугольник со стороной 17, разбитый на единичные треугольники прямыми, параллельными его сторонам. За один ход можно по линиям сетки обвести выпуклый многоугольник, при этом построенные ломаные не должны иметь общих точек. Двое ходят по очереди. Проигрывает тот, кто не может сделать ход. Кто выиграет?

Лига 11А

1. Вычислите сумму 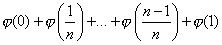, где .

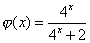2. Дан треугольник ABC. Две прямые, симметричные прямой АС относительно прямых АВ и ВС соответственно, пересекаются в точке К. Докажите, что прямая ВК проходит через центр описанной окружности треугольника АВС.

3. Докажите, что при любом n число 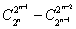делится на 4^n-1.

4. Имеется N человек, незнакомых между собой. Докажите, что при любом N их можно познакомить так, чтобы никакие трое не имели поровну знакомых.

5. Какое наибольшее число точек можно расположить на плоскости так, чтобы среди их попарных расстояний было бы только два различных?

6. Найдите все функции f(x), удовлетворяющие соотношению xf(y)+yf(x)=(x+y)f(x)f(y) при любых действительных x, y.

7. Пусть A,B,C - углы, a, b, c - стороны треугольника. Докажите неравенство .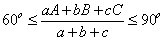

8. Существует ли правильный шестиугольник , вершины которого лежат на шести концентрических сферах, радиусы которых образуют арифметическую прогрессию?

Лига 11Б

1. Можно ли из последовательности 1, 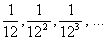выбрать числа, составляющие бесконечную геометрическую прогрессию, сумма которой равна .

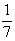2. Назовем угол выпуклого n -угольника хорошим, если его синус равен произведению синусов все остальных углов n -угольника. Какое наибольшее количество хороших углов может быть в n -угольнике? Дайте ответ для каждого из всех натуральных n.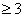

3. Докажите, что если х ⁵ + у ⁵ = х - у и х > y > 0, то х ⁴ + у ⁴ <1.

4. В вершинах куба расставлены различные числа. Каково наибольшее число тех из них, которые больше среднего арифметического своих трех соседей?

5. Из медиан прямоугольного треугольника можно составить другой прямоугольный треугольник. Докажите, что эти треугольники подобны.

6. Квадратный трехчлен W(x) = x² + ax + b с целыми коэффициентами удовлетворяет следующему условию: для каждого простого числа р существует натуральное число k такое, что числа W(k ) и W(k + 1) оба делятся на р. Докажите, что существует такое целое число т, для которого W( т ) = W( т + 1) = 0.

7. На боковых ребрах SA, SB, SC и SD правильной четырехугольной пирамиды SABСD взяты точки A₁, B₁, C₁, D₁ . Докажите, что они лежат в одной плоскости тогда и только тогда, когда расстояния a, b, c, d от них до вершины S , соответственно, удовлетворяют соотношению .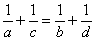

8. Аня и Боря по очереди (начинает Аня) расставляют в клетках таблицы 6´ 6 вещественные числа. Ставить число, которое уже стоит в какой-нибудь клетке, нельзя. После того, как вся таблица заполнена, в каждой строке закрашивают черным клетку с наибольшим числом. Аня выигрывает, если можно провести ломаную, соединяющую верхнюю сторону таблицы с нижней стороной и лежащую целиком в черных клетках. В противном случае выигрывает Боря. Кто выиграет при правильной игре?