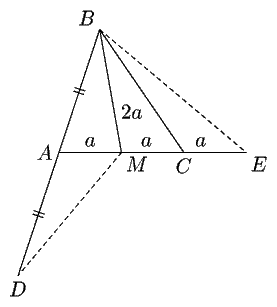
Рисунок к задаче 4 (8 кл.)
63 Московская Математическая Олимпиада прошла в воскресенье 5 марта 2000 года
Закрытие 63 ММО прошло в воскресенье 19 марта 2000 года
Архив (zip) этой странички с рисунками (94Kb) лежит здесь.
Архив (zip) книжки с условиями и решениями в формате PostScript (150Kb)
лежит здесь.
1. Два различных числа x и y (не обязательно целых) таковы, что x2-2000x=y2-2000y. Найдите сумму чисел x и y. (С. Злобин) Решение
2. В выборах в 100-местный парламент участвовали 12 партий. В парламент проходят партии, за которые проголосовало строго больше 5% избирателей. Между прошедшими в парламент партиями места распределяются пропорционально числу набранных ими голосов (т. е. если одна из партий набрала в x раз больше голосов, чем другая, то и мест в парламенте она получит в x раз больше). После выборов оказалось, что каждый избиратель проголосовал ровно за одну из партий (недействительных бюллетеней, голосов "против всех" и т. п. не было) и каждая партия получила целое число мест. При этом Партия любителей математики набрала 25% голосов. Какое наибольшее число мест в парламенте она могла получить? (Ответ объясните.) (И. Ященко) Решение
3. Длины оснований трапеции равны m см и n см (m и n - натуральные числа, m не равно n). Докажите, что трапецию можно разрезать на равные треугольники. (А. Шаповалов) Решение
4. В треугольнике ABC длина медианы BM равна длине стороны AC.
На продолжениях сторон BA и AC выбраны точки D и E соответственно,
так что выполняются равенства AD=AB и CE=CM (см. рис.). Докажите, что
прямые DM и BE перпендикулярны. (Р. Женодаров)
Решение

Рисунок к задаче 4 (8 кл.)
5. В колоде часть карт лежит "рубашкой вниз". Время от времени Петя вынимает из колоды пачку из одной или нескольких подряд идущих карт, в которой верхняя и нижняя карты лежат "рубашкой вниз", переворачивает всю пачку как одно целое и вставляет её в то же место колоды. Докажите, что в конце концов все карты лягут "рубашкой вверх", как бы ни действовал Петя. (А. Шаповалов) Решение
6. Какое наибольшее число коней можно расставить на доске 5*5 клеток, так чтобы каждый из них бил ровно двух других? (Приведите пример и объясните, почему больше коней расставить нельзя.) (М. Горелов) Решение
1. Решите уравнение
(x+1)63+(x+1)62(x-1)+(x+1)61(x-1)2+...+(x-1)63=0.
(Р. Кузнец) Решение2. В строку выписано 23 натуральных числа (не обязательно различных). Докажите, что между ними можно так расставить скобки, знаки сложения и умножения, что значение полученного выражения будет делиться на 2000 нацело. (А. Шестаков) Решение
3. Дана окружность и точка A внутри её. Найдите геометрическое место вершин C всевозможных прямоугольников ABCD, где точки B и D лежат на окружности. (М. Панов) Решение
4. Гриша записал в клетки шахматной доски числа 1, 2, 3, ..., 63, 64 в некотором порядке. Он сообщил Лёше только сумму чисел в каждом прямоугольнике из двух клеток и добавил, что 1 и 64 лежат на одной диагонали. Докажите, что по этой информации Лёша может точно определить, в какой клетке какое число записано. (А. Шаповалов) Решение
5. ABCD - выпуклый четырёхугольник. Окружности, построенные на отрезках AB и CD как на диаметрах, касаются внешним образом в точке M, отличной от точки пересечения диагоналей четырёхугольника. Окружность, проходящая через точки A, M и C, вторично пересекает прямую, соединяющую точку M и середину AB, в точке K, а окружность, проходящая через точки B, M и D, вторично пересекает ту же прямую в точке L. Докажите, что |MK-ML|=|AB-CD|. (И. Шарыгин) Решение
6. Система укреплений состоит из блиндажей. Некоторые из блиндажей
соединены траншеями, причём из любого блиндажа можно перебежать в какой-нибудь
другой. В одном из блиндажей спрятался пехотинец. Пушка может одним выстрелом
накрыть любой блиндаж. В каждом промежутке между выстрелами пехотинец
обязательно перебегает по одной из траншей в соседний блиндаж (даже если по
соседнему блиндажу только что стреляла пушка, пехотинец может туда перебежать).
Назовём систему надёжной, если у пушки нет гарантированной стратегии поражения
пехотинца (т. е. такой последовательности выстрелов, благодаря которой пушка
поразит пехотинца независимо от его начального местонахождения и последующих
передвижений).
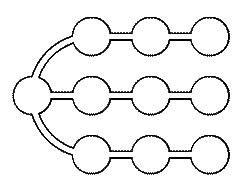
Рисунок к задаче 6 (9 кл.)
а) Докажите, что система укреплений, изображённая на рисунке, надёжна.
б) Найдите все надёжные системы укреплений, которые перестают быть
надёжными после разрушения любой из траншей.
(А. Шаповалов, А. Спивак)
Решение
1. Точки A и B взяты на графике функции y=1/x, x>0. Из них опущены перпендикуляры на ось абсцисс, основания перпендикуляров - HA и HB; O - начало координат. Докажите, что площадь фигуры, ограниченной прямыми OA, OB и дугой AB, равна площади фигуры, ограниченной прямыми AHA, BHB, осью абсцисс и дугой AB. (Р. Анно, В. Кириченко) Решение
2. Пусть f(x)=x2+12x+30. Решите уравнение
f(f(f(f(f(x)))))=0.
(М. Евдокимов) Решение3. На бумаге "в клеточку" нарисован выпуклый многоугольник, так что все его вершины находятся в вершинах клеток и ни одна из его сторон не идёт по вертикали или горизонтали. Докажите, что сумма длин вертикальных отрезков линий сетки, заключённых внутри многоугольника, равна сумме длин горизонтальных отрезков линий сетки внутри многоугольника. (Г. Гальперин) Решение
4. ABCD - выпуклый четырёхугольник. Окружности, построенные на отрезках AB и CD как на диаметрах, касаются внешним образом в точке M, отличной от точки пересечения диагоналей четырёхугольника. Окружность, проходящая через точки A, M и C, вторично пересекает прямую, соединяющую точку M и середину AB, в точке K, а окружность, проходящая через точки B, M и D, вторично пересекает ту же прямую в точке L. Докажите, что |MK-ML|=|AB-CD|. (И. Шарыгин) Решение
5.
Последовательность x1, x2, ..., xn, ... будем
обозначать {xn}. Из имеющихся последовательностей
{bn} и {cn} (возможно, {bn} совпадает с
{cn}) разрешается получать последовательности
{bn+cn}, {bn-cn},
{bn*cn} и {bn/cn}
(если все cn отличны от 0). Кроме того, из любой имеющейся
последовательности можно получить новую, вычеркнув несколько начальных членов.
Сначала есть только последовательность {an}.
Можно ли получить из неё описанными выше
операциями последовательность {n}, т. е. 1, 2, 3, 4, ..., если
а) an=n2;
б) an=n+21/2;
в) an=(n2000+1)/n ?
(А. Шаповалов, В. Доценко)
Решение
6. Из колоды вынули 7 карт, показали всем, перетасовали и раздали
Грише и Лёше по 3 карты, а оставшуюся карту
а) спрятали;
б) отдали Коле.
Гриша и Лёша могут по очереди сообщать вслух любую информацию о своих
картах. Могут ли они сообщить друг другу свои карты так, чтобы при этом Коля
не смог вычислить местонахождение ни одной из тех карт, которых он не видит?
(Гриша и Лёша не договаривались о каком-либо особом способе общения; все
переговоры происходят открытым текстом.)
(А. Шаповалов)
Решение
1. Наибольший общий делитель (НОД) натуральных чисел m и n равен 1. Каково наибольшее возможное значение НОД чисел m+2000n и n+2000m? (С. Злобин) Решение
2. Вычислите
| p | |
| т | (|sin(1999x)| - |sin(2000x)|)dx. |
| 0 |
3. Хорды AC и BD окружности с центром O пересекаются в точке K. Пусть M и N - центры окружностей, описанных около треугольников AKB и CKD соответственно. Докажите, что OM=KN. (А. Заславский) Решение
4. У Феди есть три палочки. Если из них нельзя сложить треугольник, Федя укорачивает самую длинную из палочек на сумму длин двух других. Если длина палочки не обратилась в нуль и треугольник снова нельзя сложить, то Федя повторяет операцию, и т. д. Может ли этот процесс продолжаться бесконечно? (А. Шаповалов) Решение
5.
В круговом шахматном турнире каждый участник сыграл с каждым один раз.
Назовём партию неправильной, если выигравший её шахматист в итоге набрал очков
меньше чем проигравший. (Победа даёт 1 очко, ничья - 1/2, поражение - 0.)
Могут ли неправильные партии составлять
а) более 75% от общего количества партий в турнире;
б) более 70% ?
(С. Токарев)
Решение
6. Можно ли расположить бесконечное число равных выпуклых многогранников в слое, ограниченном двумя параллельными плоскостями, так чтобы ни один многогранник нельзя было вынуть из слоя, не сдвигая остальных? (А. Канель-Белов) Решение
1. Данное в условии равенство перепишем следующим образом:
2000(x-y)=(x-y)(x+y).
Так как x не равно y, можно сократить на x-y. Отсюда x+y=2000.2. Ответ: 50 мест. Если 10 партий наберут ровно по 5% голосов, а две, включая Партию любителей математики (ПЛМ), - по 25%, то представители ПЛМ получат ровно 50 мест в парламенте. Докажем, что большее число мест ПЛМ получить не может. Действительно, количество мест, полученных ПЛМ в парламенте, равно
100*(количество голосов, набранных
ПЛМ)/(количество голосов, набранных всеми партиями,
прошедшими в парламент)=
=100*(количество голосов, набранных
ПЛМ)/((общее количество
избирателей)-(количество голосов, набранных всеми
партиями, не прошедшими в парламент))
3. Пусть m>n. Продолжим боковые стороны трапеции до пересечения и
разобьём каждую сторону получившегося треугольника на m равных частей. Через
точки деления проведём прямые, параллельные сторонам треугольника (см. рис.
8.1), и по теореме Фалеса получим разбиение треугольника на равные маленькие
треугольники. Верхнее основание трапеции является одной из проведённых линий,
так как его длина выражается целым числом сантиметров. Таким образом, мы
получили разбиение трапеции на равные треугольники.
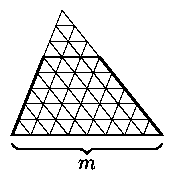
Рис. 8.1
4. Пусть K - точка, симметричная M относительно точки A.
Треугольник KMB равнобедренный (KM=MB), треугольник EMB тоже равнобедренный.
Обозначим через a величину угла при основании
треугольника KMB, через b - величину угла при
основании треугольника EMB. Так как сумма углов любого треугольника равна
180o, то
/KBE=a+b=90o
(см. рис. 8.2), т. е. KB | BE. Заметим, что четырёхугольник
DKBM - параллелограмм, т. е. DM||KB. Следовательно, DM | BE.
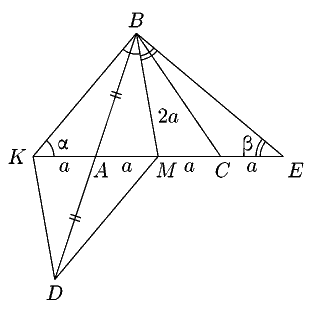
Рис. 8.2
5. Расположению карт в колоде сопоставим число, в котором цифр столько, сколько в колоде карт, причём на k-м месте справа стоит "1", если k-я карта снизу лежит рубашкой вверх, и "2" в противном случае. Тогда после каждого преобразования это число уменьшается. (Действительно, сравним полученное число с предыдущим. Среди всех цифр, которые изменились, выберем самую левую, т. е. найдём самый старший изменившийся разряд. Очевидно, в этом разряде цифра "2" сменилась на "1".) Поскольку количество n-значных чисел из единиц и двоек конечно (не больше 2n), в конце концов мы получим число, состоящее из одних единиц, что соответствует расположению всех карт рубашкой вверх.
6. На рис. 8.3 приведено расположение 16 коней, удовлетворяющее
условию задачи. Покажем, что большее число коней расставить нельзя. Раскрасим
клетки доски, как показано на рис. 8.3. Заметим, что количество коней,
расположенных на чёрных клетках, равно количеству коней, расположенных на
белых клетках. Значит, если число пустых белых клеток равно n, то число пустых
чёрных клеток равно n+1.

Рис. 8.3
При любом оптимальном расположении коней центральная клетка пуста.
В противном случае из восьми клеток, которые бьёт конь, стоящий на центральном
поле, ровно шесть пустых белых. Отсюда n>6 и число коней не
превосходит 25-n-(n+1)<12.
Разобьём белые клетки на четыре группы, как показано на рис. 8.4 (клетки
одной группы отмечены одинаковыми цифрами). Покажем, что при оптимальном
расположении по крайней мере одна клетка каждой группы пуста (отсюда будет
следовать, что n>4). Предположим противное, например, что на всех
клетках группы 3 стоят кони. Обозначим их буквами a, b и c (рис. 8.5). Конь,
стоящий на клетке a, бьёт клетки f, d и центральную. Но, как было показано
выше, центральная клетка пуста, значит, на клетках f и d стоят кони. Аналогично
можно показать, что на клетках e и g тоже стоят кони. Но тогда конь, стоящий
на клетке c, бьёт четырёх коней, расположенных на d, e, f и g, что
противоречит условию.
 |  |
| Рис. 8.4 | Рис. 8.5 |
1. Ответ: x=0. Умножим обе части уравнения на (x+1)-(x-1)=2. Тогда оно преобразуется к виду
(x+1)64-(x-1)64=0
и легко решается:(x+1)64=(x-1)64,
|x+1|=|x-1|,
2. Разобьём данные 23 числа на восемь групп из стоящих подряд чисел:
три группы по пять чисел и четыре группы по два числа (в каком порядке эти
группы расположены - неважно). Каждую группу заключим в скобки, а между
группами расставим знаки умножения. Если расставить знаки внутри каждой
группы так, чтобы результат операций в группе из двух чисел делился на 2,
а в группе из пяти чисел - на 5, то всё выражение будет делиться на
24*53=2000.
Покажем, что такая расстановка знаков в группах существует. Если числа в
группе из двух чисел разной чётности, то между ними нужно поставить знак
умножения, если одинаковой чётности - сложения. Результат, очевидно, будет
делиться на 2. Рассмотрим группу из чисел a1, a2,
a3, a4, a5, идущих именно в таком порядке.
Выпишем остатки от деления на 5 следующих пяти сумм:
a1, a1+a2, a1+a2+a3, a1+a2+a3+a4, a1+a2+a3+a4+a5.
3. Докажем, что для точки C выполняется равенство OC2=2R2-OA2, где O - центр данной окружности, R - её радиус. Введём обозначения, как показано на рис 9.1. Отрезок OC является гипотенузой в прямоугольном треугольнике с катетами x и y (см. рис. 9.1), по теореме Пифагора получаем:
OC2=x2+y2=(x2+t2)+(y2+z2)-(z2+t2).
Осталось заметить, что x2+t2=y2+z2=R2, z2+t2=OA2. Отсюда следует, что искомым ГМТ является окружность с центром O и радиусом (2R2-OA2)1/2.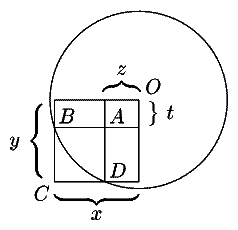
4. Пусть у Лёши есть достаточный запас доминошек $1\times 2$. Если он положит на доску две доминошки, так чтобы они перекрывались ровно по одной клетке, то, вычтя из суммы чисел под одной доминошкой сумму чисел под другой, он узнает разность чисел, накрытых ровно одной доминошкой (эти числа записаны в клетках одного цвета). Третью доминошку нужно положить так, чтобы одна её половина накрывала одно из этих двух чисел, а вторая - ещё не покрытую клетку. Складывая ранее полученную разность с суммой чисел под новой доминошкой, Лёша получит сумму тех двух чисел, которые покрыты ровно одной из трёх доминошек (эти числа записаны в клетках разного цвета). Так, добавляя всё новые и новые доминошки, можно построить цепочку, соединяющую любые две клетки доски, и, если эти клетки одного цвета, узнать их разность, а если разного - их сумму. Известно, что числа 1 и 64 расположены на одной диагонали, т. е. в клетках одного цвета. Их разность равна 63, а разность любых двух других натуральных чисел между 1 и 64 меньше 63. Поэтому Лёша может определить, в каких клетках записаны 1 и 64. Он пока не знает только, в какой из этих клеток какое число записано. Зато он знает сумму числа в каждой из этих двух клеток с любым числом, записанным в клетке другого цвета. Для клетки с числом 1 все эти суммы не превосходят 64, а для клетки с числом 64 - не меньше 66. Так что Лёша может определить, где именно записано 64. Теперь, зная сумму (или разность) числа 64 с числом в любой другой клетке, Лёша легко определит, где какое число записано.
5. Пусть P и Q - середины AB и CD, O1 и O2 -
центры окружностей, проходящих через точки A, M, C и B, M, D соответственно,
H1 и H2 - проекции O1 и O2 на
прямую PQ (рис. 9.2).
1o. Точки M, P и Q лежат на одной прямой. В самом деле, прямые
PM и QM содержат радиусы окружностей, касающихся в точке M, и, следовательно,
перпендикулярны общей внутренней касательной к этим окружностям.
2o. P и Q лежат на окружности с диаметром
O1O2. Действительно,
PO1 | PO2, поскольку эти прямые -
серединные перпендикуляры к отрезкам MB и MA, угол между которыми прямой
(M лежит на окружности с диаметром AB). Аналогично,
QO1 | QO2.
3o. Ясно, что KH1=H1M,
LH2=H2M (диаметр, перпендикулярный хорде, делит её
пополам).
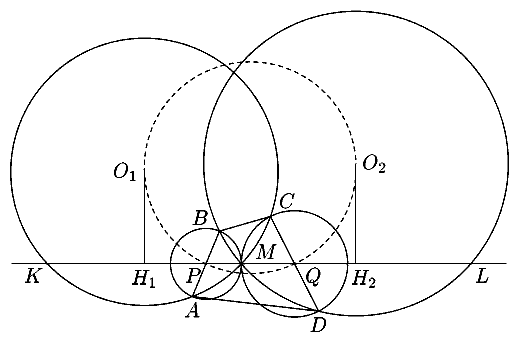
Рис. 9.2
4o. PH1=QH2, так как проекция середины отрезка
O1O2 делит отрезок H1H2 пополам, но
эта проекция делит пополам и отрезок PQ. Наконец,
|MK-ML|=2|MH1-MH2|=2|MP-MQ|=2((1/2)AB-(1/2)CD|=|AB-CD|.
6. а) Докажем, что указанная в условии система укреплений (будем
называть её трилистником) надёжна. Обозначим блиндажи, как показано на
рисунке 9.3. Ограничим начальные положения пехотинца блиндажами O,
A2, B2 и C2 (эти блиндажи мы будем называть
чётными, а остальные - нечётными). Мы считаем, что пехотинец настолько удачлив,
что спасается, если только это возможно.
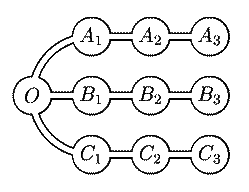
Рис. 9.3
Заметим, что выстрел пушки по одному из нечётных блиндажей заведомо бесполезен.
Если пушка выстрелит по блиндажу O (удачливый пехотинец, конечно, не там), то
из оставшихся трёх чётных блиндажей пехотинец сможет перебежать в любой из
шести нечётных. Теперь, если пушка выстрелит по одному из этих нечётных
блиндажей, то пехотинец из оставшихся пяти сможет перебежать в любой из четырёх
чётных. Таким образом, повторится начальная расстановка.
| Поражённый блиндаж | Пехотинец |
| O любой блиндаж | B1, B3, C1, C3 O, B2, C2 |
| B2 (для C2 - то же) A1 (для B1 - то же) | A1, B1, C1, C3 O, B2, C2 |
| B2 (для C2 - то же) C1 или C3 | A1, B1, C1, C3 O, A2, B2, C2 |
1. Можно считать, что абсцисса точки A меньше абсциссы точки B
(рис. 10.1). Рассмотрим точку K пересечения отрезков AHA и OB.
Тогда разность рассматриваемых площадей равна разности площадей треугольника
OAK и четырёхугольника HAKBHB, которая, в свою очередь,
равна разности площадей треугольников OAHA и OBHB.
А поскольку OHA*AHA=OHB*BHB=1
(вспомните, что A и B лежат на графике), эти площади равны между собой.
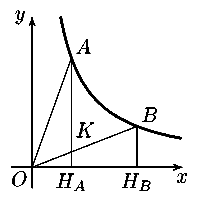
Рис. 10.1
2. Заметим, что
f(x)=(x+6)2-6.
Отсюда видно, чтоf(f(f(f(f(x))))) = (x+6)32-6.
Осталось выписать ответ: x = -6 + 61/32.3. Докажем, что каждая из рассматриваемых величин равна площади многоугольника. Проверим это для суммы длин горизонтальных отрезков. Проведём эти отрезки. Тогда многоугольник разобьётся на два треугольника и несколько трапеций, причём высоты этих фигур будут равны 1. Осталось выразить площади этих фигур через основания и высоты по известной формуле и сложить. Видно, что каждый горизонтальный отрезок войдёт в сумму два раза, то есть с коэффициентом единица, что и требовалось.
4. См. решение задачи 5 варианта 9 класса.
5. Ответ: а), в) можно; б) нельзя.
Объясним, как можно действовать в пунктах а) и в).
Очевидно, что разрешёнными операциями можно получить из последовательности
{an} последовательность {an+1-an$. Такое
преобразование обозначим через T, а m-кратное применение преобразования T
обозначим через Tm. Заметим, что если P(n) - многочлен от n
степени m-1, то применение T к последовательности {P(n)} даёт
последовательность {Q(n)}, где Q(n) - многочлен степени m-2. Отсюда, в
частности, следует, что применение Tm к {P(n)} даёт нулевую
последовательность. Ещё нам пригодится последовательность I, все члены
которой - единицы (её можно получить делением данной последовательности на
себя). Теперь легко предъявить последовательность операций для каждого из
пунктов:
| {n2} | T | {2n+1} | -I | {2n} | /(I+I) | {n} | |
| а) | ® | ® | ® | ; | |||
| в) | { | n2000+1 | } | T2000 | { | 2000! | } | I/ | { | n(n+1)*...*(n+2000) | } | *(2000!*I) | T2000 | |
| ------ | ® | -------------- | ® | -------------- | ® | {n(n+1)*...*(n+2000)} | ® | {an+b} | , | |||||
| n | n(n+1)*...*(n+2000) | 2000! |
6. а) Пусть Гриша скажет: "У меня либо {называет свои карты}, либо {называет три карты, которых у него нет}". После этого Лёша должен сказать: "У меня либо {называет свои карты}, либо {называет три карты Гриши, если второй из наборов, названных Гришей, не совпадает с его набором, и любые другие три карты, которых у него нет, иначе}". После этого каждый из них, очевидно, знает весь расклад. Коле же ничего не ясно. Действительно, названо три набора карт: A, B и C. Наборы B и C пересекаются по двум картам, Гриша сказал: "У меня либо A, либо B", Лёша сказал: "У меня либо A, либо C". Это означает, что либо у Гриши набор A, а у Лёши - C, либо у Гриши - B, а у Лёши - A. Конечно, эти расклады различны, и даже закрытую карту определить нельзя. б) Заметим, что предыдущий способ не работает: зная закрытую карту, Коля может всё определить. Занумеруем карты числами от 0 до 6. Пусть Гриша и Лёша по очереди назовут остатки от деления суммы номеров своих карт на 7. Тогда они узнают расклад: каждый из них должен лишь прибавить к своей сумме сумму другого и найти остаток, противоположный этой общей сумме по модулю 7 (т. е. такой, который при прибавлении к этой сумме даёт число, делящееся на 7). Это и будет номер закрытой карты. После этого восстановление расклада не составляет труда. Проверим, что Коля ничего не узнал. Рассмотрим карту с номером s. Покажем, что она могла попасть к Грише, если он назвал сумму a. Для этого надо дополнить эту карту двумя другими с суммой номеров a-s. Легко видеть, что существует три различные пары номеров, дающие в сумме a-s. Из них две, возможно, испорчены тем, что туда входит карта с номером s или закрытая карта, но как минимум одна пара остаётся. Ей мы и дополним набор Гриши. Такие же рассуждения показывают, что любая карта могла оказаться и у Лёши.
1. Ответ: 20002-1. Пусть a=2000m+n, b=2000n+m, d - наибольший общий делитель a и b. Тогда d делит также числа
2000a-b=(20002-1)m и 2000b-a=(20002-1)n.
Поскольку m и n взаимно просты, то d делит 20002-1. С другой стороны, при m=20002-2000-1, n=1, получаем a=(20002-1)(2000-1), b=20002-1=d.2. Ответ: 0. График функции |sin(kx)| на отрезке [0;p] состоит из k одинаковых "шапочек", которые получаются из графика функции sin x на том же отрезке путём сжатия к оси ординат в k раз. При этом площадь под графиком также уменьшается в k раз. Как следствие, площадь под k "шапочками" одинакова при любом k.
3. Пусть X - середина KB.
Тогда /KMX=(1/2)/KMB=/KAB=/KDC. Поскольку
MX | BD, то KM | CD. Так как при этом
ON | CD, ON||KM. Аналогично, OM||KN.
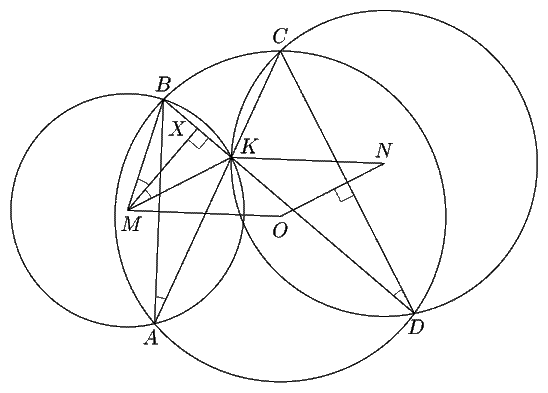
Рис. 11.1
Если точки O, K, M, N не лежат на одной прямой, то OMKN - параллелограмм и
OM=KN. В противном случае рассмотрим ортогональные проекции отрезков OM и KN
на AC. Так как точки O, M, N проектируются соответственно в середины отрезков
AC, AK, KC, то проекции обоих параллельных отрезков равны (1/2)KC.
Следовательно, равны и длины самих отрезков.
4. Ответ: может. Многочлен P(x)=x3-x2-x-1 имеет корень t, больший 1, поскольку P(1)<0, а $P(2)>0. Тогда t3=t2+t+1>t2+t. Возьмём длины палочек равными t3, t2, t. После первого отпиливания получим палочки с длинами t2, t, 1. Так как отношение длин не изменилось, процесс будет продолжаться бесконечно.
5. Ответ: а) не могут; б) могут.
а) Пусть N - число игроков, M=[N/2]. Игроков, занявших первые M мест,
назовём сильными, а остальных - слабыми (между участниками с одинаковой суммой
очков места распределяются произвольно). Пусть X - число правильных партий
между сильными и слабыми. Сумма очков, набранных сильными во встречах между
собой, равна M(M-1)/2, а во встречах со слабыми - не больше X. Поэтому средний
результат сильного не больше ((M-1)/2)+(X/M). Аналогично, средний результат
слабого не меньше ((N-M-1)/2)+((M(N-M)-X)/(N-M)). Если есть неправильные
партии, то не все игроки набрали поровну, и средний результат сильного больше,
чем слабого. Отсюда X>M(N-M)/2>N(N-1)/8. Так как общее число
партий равно N(N-1)/2, доля правильных партий больше 1/4.
б) Возьмём сначала турнир 2k+1 игрока, в котором каждый участник с
номером i<k проиграл участникам с номерами i+1, ..., i+k и
выиграл у остальных, а каждый участник с номером i>k выиграл у участников
с номерами i-k, ..., i-1 и проиграл остальным. Очевидно, что все игроки набрали
по k очков, причём в таблице турнира выше главной диагонали единицы стоят лишь
в k(k+1)/2 клетках из 2k(2k+1)/2. Теперь "размножим" каждого игрока, заменив
его блоком из n новых, и пусть участники из разных блоков играют друг с другом
так же, как соответствующие прежние участники, а участники из одного блока
играют друг с другом вничью. Получим новую таблицу, в которой по-прежнему у
всех игроков поровну очков. Исправим эту таблицу так, чтобы суммы очков игроков
перестали быть равными. Для этого будем менять результаты участников из блока
k+1: в их встречах против участников из блока k+1-i заменим i*n выигрышей
ничьими, так что сумма очков каждого участника блока k+1 уменьшится, а
каждого участника блока k+1-i увеличится на i/2. Напротив, в партиях с игроками
блока k+1+i заменим ничьими i*n проигрышей. Число неправильных партий станет
равно n2(2k(2k+1)/2)-n2(k(k+1)/2)-2n(k(k+1)/2).
При этом общее число партий равно n(2k+1)(n(2k+1)-1)/2.
При n=k=20 неправильные партии составляют 235,600/335,790>0,7 от общего
числа партий.
6. Будем помещать между плоскостями правильные тетраэдры, расстояние
между противоположными рёбрами которых равно расстоянию между плоскостями.
Пусть одно из рёбер каждого тетраэдра лежит в одной из граничных плоскостей,
а противоположное ему - в другой. Два тетраэдра можно расположить так, чтобы
конец "верхнего" ребра первого совпадал с серединой "верхнего" ребра второго,
а середина "нижнего" ребра первого - с концом "нижнего" ребра второго, и при
этом как "верхние", так и "нижние" рёбра обоих тетраэдров были перпендикулярны.
Распространив этот процесс на весь слой, получим, что каждый тетраэдр окружён
четырьмя другими (рис. 11.2); два из них не позволяют выдвинуть его "вверх",
два остальных - "вниз".
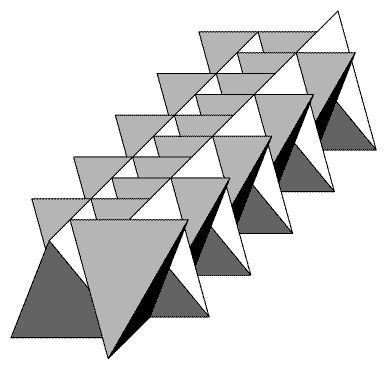
Рис. 11.2
Дата последнего обновления: 31 января 2001 г.