10 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Известно, что b – c > a и а ≠ 0. Обязательно ли уравнение ax2 + bx + c = 0 имеет два корня?
1.2. В выпуклом пятиугольнике равны все стороны, а также равны четыре из пяти диагоналей. Следует ли из этого условия, что пятиугольник – правильный?
1.3. Найдите все натуральные n и k, удовлетворяющие равенству: k5 + 5n4 = 81k.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Существует ли такое натуральное n, что 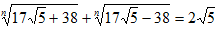 ?
?
2.2. В выпуклом четырёхугольнике ABCD отмечены середины противоположных сторон BC и AD – точки M и N. Диагональ AC проходит через середину отрезка MN. Найдите площадь АВСD, если площадь треугольника АВС равна S.
2.3. Девять лыжников ушли со старта по очереди и прошли дистанцию – каждый со своей постоянной скоростью и финишировали в разное время. Могло ли оказаться так, что каждый лыжник участвовал ровно в четырёх обгонах? (В каждом обгоне участвуют ровно два лыжника – тот, кто обгоняет, и тот, кого обгоняют.)
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Существует ли такая функция f(x), определенная для всех действительных чисел, что f(sin x) + f(cos x) = sin x?
3.2. Параллелограмм и квадрат расположены так, что вершины квадрата лежат на сторонах параллелограмма (по одной вершине на каждой стороне). Из каждой вершины параллелограмма проведена прямая перпендикулярная ближайшей стороне квадрата. Докажите, что точки попарного пересечения этих прямых также являются вершинами квадрата.
3.3. Изначально на экране компьютера – какое-то простое число. Каждую секунду число на экране заменяется на число, полученное из предыдущего прибавлением его последней цифры, увеличенной на 1. Через какое наибольшее время на экране возникнет составное число?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Числа а, b и с лежат в интервале (0; 1).
Докажите, что a + b + c + 2abc > ab + bc + ca + 2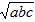 .
.
4.2. В треугольник АВС вписана окружность. Из середины каждого отрезка, соединяющего две точки касания, проводится перпендикуляр к противолежащей стороне. Докажите, что эти перпендикуляры пересекаются в одной точке.
4.3. Какое наименьшее количество цветов необходимо, чтобы покрасить все вершины, стороны и диагонали выпуклого n-угольника, если должны выполняться два условия:
1) любые два отрезка, выходящие из одной вершины должны быть разного цвета;
2) цвет любой вершины должен отличаться от цвета любого отрезка, выходящего из нее?