8 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. В выражении x6 + x4 + x·A замените А на одночлен так, чтобы получился полный квадрат. Найдите как можно больше решений.
1.2. На свой день рождения Василиса купила треугольный пирог, который она разрезала по каждой биссектрисе и получилось 6 кусков. Опоздавшему Игорю достался кусок в форме прямоугольного треугольника, на основании чего он заявил, что пирог имел форму равнобедренного треугольника. Прав ли Игорь?
1.3. Найдите наименьшее натуральное n, для которого (n + 1)(n + 2)(n + 3)(n + 4) делится на 1000.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. На перемене несколько учащихся ушли из лицея и несколько пришли в него. В результате количество учеников в лицее после перемены уменьшилось на 10%, а доля мальчиков среди учеников лицея увеличилась с 50% до 55%. Увеличилось или уменьшилось количество мальчиков?
2.2. Высота АН остроугольного треугольника АВС равна его медиане ВМ. На продолжении стороны АВ за точку В отложена точка D так, что BD = AB. Найдите угол BCD.
2.3. Можно ли из кубиков размером 1×1×1 склеить многогранник, площадь поверхности которого равна 2015? (Кубики приклеиваются так, что склеиваемые грани полностью примыкают друг к другу.)
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Петя записал несколько алгебраических выражений, возвёл каждое из них в квадрат и сложил результаты. Могло ли у него в итоге получиться выражение x2 + y2 + z2 + 3y + 4x + xz + 1?
3.2. Внутри ромба АВСD выбрана точка N так, что треугольник ВСN – равносторонний. Биссектриса BL треугольника ABN пересекает диагональ АС в точке K. Докажите, что точки K, N и D лежат на одной прямой.
3.3. Сколько существует несократимых дробей с числителем 2015, меньших, чем 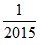 и больших,
чем
и больших,
чем 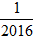 ?
?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Известно, что а > 1. Обязательно ли имеет место равенство: 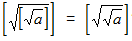 ?
(Напомним, что [x] – это целая часть числа x, то есть это наибольшее целое число, не превосходящее x.)
?
(Напомним, что [x] – это целая часть числа x, то есть это наибольшее целое число, не превосходящее x.)
4.2. На боковых сторонах AB и BC равнобедренного треугольника ABC отмечены точки E и F соответственно так, что AE = 2BF. На луче EF отмечена точка G так, что GF = EF. Докажите, что угол ACG – прямой.
4.3. Напомним, что игра в «морской бой» начинается с того, что на доске размером 10×10 клеток расставляют один «корабль» из четырех клеток, два – из трех клеток, три – из двух, и четыре одноклеточных (такие, как на рисунке). По правилам, «корабли» не должны касаться, даже углами. До какого наименьшего размера можно уменьшить поле для игры, оставив его квадратным и сохранив это правило?
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | Сумма | Диплом | ||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| 2 А | 4 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 88 | I |
| ГМК А | 4 | 6 | 6 | 7 | 1 | 7 | 8 | 8 | 8 | 9 | 9 | 4 | 77 | II |
| Интеллектуал А | 4 | 6 | 6 | 7 | 7 | 7 | 0 | 8 | 8 | 0 | 9 | 9 | 71 | II |
| 1543 А | 3 | 3 | 6 | 7 | 0 | 7 | 8 | 0 | 8 | 0 | 9 | 9 | 60 | III |
| 179 Б | 3 | 6 | 6 | 7 | 7 | 7 | 0 | 0 | 8 | 0 | 2 | 9 | 55 | III |
| ГМК Б | 4 | 6 | 3 | 7 | 1 | 7 | 0 | 0 | 8 | 0 | 9 | 8 | 53 | III |
| Интеллектуал Б | 2 | 6 | 6 | 7 | 0 | 7 | 0 | 0 | 7 | 9 | 0 | 9 | 53 | III |
| 1534 А | 4 | 3 | 6 | 7 | 7 | 7 | 0 | 0 | 0 | 0 | 9 | 9 | 52 | III |
| 9 | 0 | 0 | 1 | 7 | 7 | 7 | 8 | 0 | 3 | 9 | 0 | 9 | 51 | III |
| 1543 В | 2 | 6 | 6 | 7 | 1 | 7 | 0 | 6 | 2 | 0 | 9 | 4 | 50 | III |
| 2 Б | 4 | 6 | 5 | 7 | 1 | 7 | 0 | 8 | 8 | 0 | 0 | 4 | 50 | III |
| 1568 Д | 3 | 6 | 3 | 7 | 1 | 7 | 0 | 8 | 0 | 0 | 9 | 4 | 48 | ПП |
| 179 В | 2 | 0 | 3 | 7 | 0 | 7 | 8 | 0 | 0 | 0 | 9 | 9 | 45 | ПП |
| 5 Б Долгопрудный | 3 | 0 | 6 | 7 | 1 | 7 | 0 | 1 | 8 | 0 | 0 | 9 | 42 | ПП |
| 5 А Долгопрудный | 2 | 4 | 3 | 7 | 1 | 7 | 0 | 0 | 8 | 0 | 0 | 9 | 41 | ПП |
| ЛНИП А Королев | 1 | 2 | 6 | 7 | 1 | 7 | 0 | 0 | 8 | 0 | 0 | 9 | 41 | ПП |
| 2086 | 4 | 6 | 1 | 7 | 0 | 0 | 0 | 0 | 3 | 0 | 9 | 9 | 39 | |
| 533 (ЮМШ) СПб | 4 | 0 | 6 | 7 | 1 | 7 | 0 | 0 | 5 | 0 | 0 | 9 | 39 | |
| ЛНИП Б Королев | 4 | 1 | 6 | 7 | 0 | 7 | 0 | 0 | 1 | 0 | 0 | 9 | 35 | |
| 2007 Д | 3 | 1 | 3 | 7 | 0 | 7 | 0 | 0 | 4 | 0 | 0 | 9 | 34 | |
| 366 А СПб | 4 | 6 | 3 | 7 | 0 | 3 | 0 | 1 | 1 | 0 | 9 | 0 | 34 | |
| 1514 А | 2 | 0 | 6 | 7 | 0 | 7 | 0 | 0 | 2 | 0 | 0 | 9 | 33 | |
| Физтех-лицей А | 4 | 1 | 4 | 7 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 9 | 33 | |
| 179 А | 0 | 0 | 6 | 7 | 1 | 0 | 0 | 0 | 8 | 0 | 0 | 9 | 31 | |
| 2007 А | 4 | 3 | 6 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 4 | 31 | |
| 2007 Г | 4 | 1 | 6 | 7 | 1 | 7 | 0 | 0 | 1 | 0 | 0 | 4 | 31 | |
| 1568 Б | 2 | 3 | 6 | 7 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 9 | 30 | |
| 2007 Б | 3 | 1 | 6 | 7 | 1 | 3 | 0 | 0 | 0 | 0 | 0 | 9 | 30 | |
| 1514 Б | 3 | 6 | 0 | 7 | 1 | 0 | 8 | 0 | 0 | 0 | 0 | 4 | 29 | |
| 853 В | 0 | 3 | 0 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 9 | 9 | 29 | |
| 1189 Б | 4 | 2 | 6 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 28 | |
| 1537 | 1 | 3 | 6 | 7 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 4 | 28 | |
| 1568 Г | 3 | 3 | 6 | 7 | 0 | 7 | 0 | 0 | 2 | 0 | 0 | 0 | 28 | |
| 2 Г | 2 | 3 | 1 | 7 | 0 | 1 | 8 | 0 | 2 | 0 | 0 | 4 | 28 | |
| 366 Б СПб | 1 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 5 | 0 | 0 | 9 | 28 | |
| 171 (54) В | 4 | 3 | 1 | 7 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 4 | 27 | |
| 1514 В | 1 | 2 | 6 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 26 | |
| 1568 А | 1 | 1 | 6 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 4 | 26 | |
| 853 Б | 1 | 0 | 6 | 7 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 4 | 26 | |
| 1534 В | 1 | 0 | 6 | 7 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 4 | 25 | |
| Инт.-6 А Мытищи | 2 | 0 | 6 | 7 | 1 | 3 | 0 | 0 | 2 | 0 | 0 | 4 | 25 | |
| 444 А | 1 | 0 | 6 | 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 9 | 24 | |
| ГСГ А | 5 | 0 | 0 | 0 | 1 | 4 | 0 | 0 | 5 | 0 | 8 | 1 | 24 | |
| Физтех-лицей В | 2 | 5 | -1 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 4 | 24 | |
| 171 (54) Б | 1 | 1 | 1 | 7 | 1 | 3 | 0 | 0 | 8 | 0 | 0 | 1 | 23 | |
| 30 Б СПб | 2 | 5 | 0 | 5 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 4 | 23 | |
| СВМ А Мытищи | 3 | 0 | 6 | 7 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 4 | 23 | |
| 1189 Г | 1 | 0 | 0 | 7 | 1 | 7 | 0 | 0 | 0 | 2 | 0 | 4 | 22 | |
| 2 В | 2 | 6 | 0 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 22 | |
| 2101 Б | 2 | 1 | 0 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 4 | 21 | |
| Подольск | 4 | 2 | -1 | 7 | 1 | 6 | 0 | 0 | 2 | 0 | 0 | 0 | 21 | |
| 1208 | 3 | 1 | 0 | 7 | 0 | 3 | 0 | 0 | 2 | 0 | 0 | 4 | 20 | |
| 30 А СПб | 1 | 0 | 0 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 18 | |
| 1581 Б | 3 | 1 | 0 | 7 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 17 | |
| 218 А | 2 | 2 | 0 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 17 | |
| ГСГ Б | 2 | 1 | 0 | 7 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 4 | 17 | |
| НГШ | 0 | 1 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 17 | |
| 1189 А | 2 | 0 | 3 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 16 | |
| 171 (54) А | 1 | 1 | 0 | 2 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 4 | 16 | |
| 1534 Б | 3 | 1 | 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 15 | |
| 1581 В | 2 | 0 | 0 | 5 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 15 | |
| 444 В | 0 | 0 | 0 | 7 | 1 | 3 | 0 | 0 | 0 | 0 | 0 | 4 | 15 | |
| 82 Черноголовка | 1 | 2 | 0 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 15 | |
| 1543 Б | 0 | 0 | 6 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | |
| 218 В | 4 | 1 | 0 | 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 14 | |
| 444 Б | 1 | 1 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 13 | |
| 853 А | 0 | 1 | 0 | 7 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 13 | |
| 1568 В | 1 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 12 | |
| 218 Б | 2 | 1 | 0 | 0 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 12 | |
| Физтех-лицей Б | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 4 | 12 | |
| 1468 А | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 11 | |
| 2007 В | 2 | 1 | 0 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | |
| 2033 А | 2 | 1 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 11 | |
| 444 Г | 2 | 1 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 11 | |
| 1189 В | 2 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | |
| 1581 А | 1 | 1 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | |
| 2033 Б | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 8 | |
| 879 Б | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 7 | |
| Троицк | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 7 | |
| 879 А | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 6 | |
| 1434 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 5 | |
| 1468 В | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 5 | |
| 171 (54) Г | 0 | 0 | 0 | 5 | 1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | |
| СВМ Б Мытищи | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 5 | |
| 2101 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 4 | |
| Снегири | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 4 | |
| Инт.-6 Б Мытищи | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 3 | |
| 1468 Б | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |