11 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите уравнение: 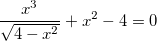
1.2. Существует ли многоугольник, в котором каждая сторона равна одной из диагоналей, а каждая диагональ равна какой-то стороне?
1.3. На бесконечной шахматной доске стоят два ферзя, не бьющие друг друга. Сколько на доске клеток, которые находятся под боем обеих фигур?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Вычислите: (1 + tg5°)(1 + tg10°)(1 + tg15°)(1 + tg20°)(1 + tg25°)(1 + tg30°)(1 + tg35°)(1 + tg40°)
2.2. Биссектриса угла A остроугольного треугольника ABC пересекает окружность, описанную около этого треугольника, в точке D. Сумма расстояний от вершин B и C до прямой AD в два раза меньше AD. Найдите угол BAC.
2.3. Петя записал на доске пять трехзначных простых чисел. Обязательно ли среди них найдутся два числа с разностью, кратной 12?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Известно, что x4y2 + x2 + 2x3y + 6x2y + 8 ≤ 0. Докажите, что 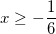
3.2. В правильной четырехугольной пирамиде ребро основания равно 6, высота равна 4. Найдите площадь ортогональной проекции этой пирамиды на плоскость боковой грани.
3.3. Найдите все целые решения уравнения 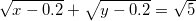
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Существуют ли такие функции f и g, определенные на R и отличные от постоянных, что g(x) – четная функция, а g(f(x)) – нечетная?
4.2. Отрезок EF разбивает четырехугольник ABCD на два равновеликих четырехугольника AEFD и BEFC, каждый из которых является вписанным. Найдите длину EF, если ВС = 1, AD = 7.
4.3. Оля и Коля играют в следующую игру: Оля называет два натуральных числа а и b, а Коля должен так подобрать натуральное число k, чтобы числа ka и kb имели одинаковую сумму цифр. Всегда ли Коля сможет это сделать?
Пятый тур (15 минут; каждая задача – 7 баллов).