11 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Найдите наименьшее значение функции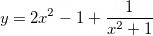 
1.2. Каждая сторона четырехугольника меньше, чем 7. Обязательно ли его площадь меньше, чем 50?
1.3. Верно ли, что число 2202 + 1 делится на 2101 + 251 + 1?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Пусть d(x) – расстояние от x до ближайшего целого числа. Сколько корней имеет уравнение d(x) = 0,001x
2.2. В треугольнике АВС через середину биссектрисы BD проведена прямая, перпендикулярная биссектрисе и пересекающая прямую АС в точке Е. Докажите, что DE2 = AE⋅EC.
2.3. В круговом шахматном турнире каждый участник выиграл белыми столько же партий, сколько все остальные в сумме выиграли черными. Верно ли, что у всех участников одинаковое количество побед?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Найдите значение параметра а, для которого уравнение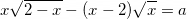 
имеет единственный корень.
3.2. Куб, длина ребра которого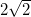 
, пересечён плоскостью. Найдите площадь сечения, если какие-то две стороны этого сечения равны 4 и 2.
3.3. Даны 11 гирь попарно различного веса и каждая весит целое число граммов. Известно, что как бы ни разложить гири (все или часть) на две чаши, чтобы гирь на них было не поровну, всегда перевесит чаша, на которой гирь больше. Докажите, что хотя бы одна из гирь весит больше, чем 35 граммов.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Найдите наименьшее значение выражения (x – y)2 + 3(y – z)2 – 5(z – x)2, если x∊[–1; 1], y∊[–1; 1], z∊[–1; 1].
4.2. Найдите геометрическое место центров правильных треугольников, вершины которых лежат на сторонах данного квадрата со стороной 1.
4.3. Существует ли восьмизначное число, являющееся точным квадратом, цифры которого идут в возрастающем порядке?
Пятый тур (15 минут; каждая задача – 7 баллов).
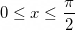. Докажите, что xsinx + cosx ≥ 1.