Условия задач II творческого конкурса учителей
(также можно скачать условия в формате PDF(132KB) или zip-архив(90KB))
Вам предлагается четыре блока заданий:
I. Решите задачи:
1. – 4. Задачи для решения.
5. – 7. Поиск математических ошибок в текстах.
8. – 9. Задачи, в которых требуется найти как можно больше способов решения.
10. Найти как можно больше ошибок в "доказательстве" теоремы Ферма
1) Две хозяйки покупали молоко каждый день в течение месяца. Цена на молоко ежедневно менялась. Средняя цена молока за месяц оказалась равной 20 рублям. Ежедневно первая хозяйка покупала по одному литру, а вторая – на 20 рублей. Кто из них потратил за этот месяц больше денег и кто купил больше молока?
2) Биссектрисы углов треугольника АВС пересекают описанную окружность в точках A’, B’ и C’. Докажите, что АА’ + BB’ + CC’ больше периметра треугольника.
3) Решите уравнение: ![]() =
= ![]() .
.
4) На концах отрезка записано по единице. На каждом шаге между каждыми двумя соседними числами вписывают их сумму. То есть, на первом шаге между двумя единицами записывают 2, на втором шаге дописывают две тройки, и так далее. Сделано 2005 шагов. Сколько раз среди выписанных чисел встретится число 2005?
II. Перед Вами тексты, которые могут содержать математические ошибки. Ошибки могут быть как в формулировках утверждений, так и в их доказательствах (решениях). В случае, если доказываемое утверждение верно, укажите ошибки в доказательстве (решении). Если утверждение неверно, объясните, почему это так, и найдите ошибку в приведенном доказательстве.
5) Решите уравнение: ![]() .
.
Решение. Перепишем данное уравнение в виде ![]() . Тогда x = –1 – корень уравнения. Кроме того,
. Тогда x = –1 – корень уравнения. Кроме того, ![]() Û
Û
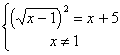 . Полученная система решений не имеет. Ответ: –1.
. Полученная система решений не имеет. Ответ: –1.
6) Теорема. Если возрастающая функция дифференцируема на некотором интервале, то в каждой точке этого интервала ее производная положительна.
Доказательство. Пусть функция f(x) имеет производную в каждой точке x0 некоторого интервала I. Тогда ![]() . Так как f(x) возрастает на интервале I, то при x > x0 получим, что f(x) > f(x0), а при x < x0 получим, что f(x) < f(x0). В обоих случаях рассматриваемая дробь положительна, поэтому f’(x0) > 0. Таким образом, в любой точке интервала I производная положительна, что и требовалось доказать.
. Так как f(x) возрастает на интервале I, то при x > x0 получим, что f(x) > f(x0), а при x < x0 получим, что f(x) < f(x0). В обоих случаях рассматриваемая дробь положительна, поэтому f’(x0) > 0. Таким образом, в любой точке интервала I производная положительна, что и требовалось доказать.
7) Теорема. Сумма плоских углов трехгранного угла меньше, чем 360° .
Доказательство. Проведем плоскость a , пересекающую все ребра данного трехгранного угла с вершиной Р, но не перпендикулярную ни одному из них и не перпендикулярную ни одной из граней этого угла. Пусть a пересекает ребра трехгранного угла в точках А, В и С.
Рассмотрим Р’ – ортогональную проекцию точки Р на плоскость a . Тогда проекциями плоских углов АРВ, ВРС и СРА трехгранного угла служат углы АР’В, ВР’С и СР’А соответственно. Так как ортогональная проекция угла, стороны которого пересекают плоскость проекции, больше самого угла, то Ð АРВ + Ð ВРС + Ð СРА < Ð АР’В + Ð ВР’С + Ð СР’А.
Исходя из способа построения плоскости a , возможны два случая: 1) Р’ лежит внутри треугольника АВС; 2) Р’ лежит вне треугольника АВС. В первом случае сумма углов АР’В, ВР’С и СР’А равна 360° , а во втором случае она меньше, чем 360° . Следовательно, искомая сумма плоских углов меньше, чем 360° , что и требовалось доказать.
III. Найдите как можно больше способов решения каждой задачи и запишите эти решения так, как Вы бы хотели их видеть в работе Вашего ученика. (Различными считаются способы, использующие различные математические идеи, а также различные технические приемы реализации одной и той же идеи.)
8) Сравните числа: ![]() и
и ![]() .
.
9) Дано: D
АВС; EÎ
[AC], |AE| : |EC| = 3 : 4; MÎ
[BC], |BM| = |MC|; (AM) ![]() (BE) = O.
(BE) = O.
Найти: |EO| : |OB|.
IV. В августе 2005 года в “Новой газете” было опубликовано “новое доказательство” великой теоремы Ферма. Найдите как можно больше математических ошибок в этом тексте.
10. Итак, требуется доказать, что если X и Y — целые числа в уравнении Xn + Yn = Zn, то Z (при n > 2) всегда не целое. Прежде чем браться за теорему Ферма, повторим теорему Пифагора: “Квадрат гипотенузы равен сумме квадратов катетов”. Мы вправе для ее написания использовать любые переменные. Запишем ее таким образом: X2 + Y2 = R2, где X, Y, R — целые числа, а Z, утверждает Ферма, — не целое. Попробуем доказать. Понятно, Z не равно R при одних и тех же X, Y. Легко доказуемо алгебраически, да и просто логически, что Z всегда меньше, чем R. Когда мы возводим X и Y в более высокую степень, то умножаем их на самих себя. Потом их складываем и получаем Z в той же степени n. А при возведении в нее R каждое из слагаемых надо умножить на R, которое больше, чем X и Y. К примеру, R3 = (X2 + Y2)R = X2R+Y2R.
Записываем длины сторон треугольника XYR в тригонометрическом виде: X = R sinA, Y = R cosA. А значит, Zn = Xn + Yn = Rn (sinA + cosA). Тогда Z = R (sinA + cosA). Ранее мы доказали, что Z всегда меньше R, стало быть, sinA + cosA < 1. Такую тригонометрическую функцию можно найти в любом учебнике математики старших классов и убедиться по графику или таблице, что если значение функции меньше 1, то угол A больше 60° и меньше 90° . А что произойдет в этом случае с прямым углом В, находящимся между катетами? Он больше уже не будет прямым и окажется в тех же пределах: 60o < B < 90o.
Любой десятиклассник, у которого по математике выше тройки, с ходу воспроизведет вам формулу соотношения сторон треугольника Z2 = X2 + Y2 — 2 XY cosB. При 60o < B < 90o cosB — число не целое. А значит, и Z неминуемо является таковым при целых значениях X и Y. Что и требовалось доказать.