15-й Математический Праздник.
15 февраля 2004 года

Условия и решения задач.

7 класс

Задача 1. [4 балла]
Ваня задумал простое трёхзначное число, все цифры которого различны. На какую цифру оно может оканчиваться, если его последняя цифра равна сумме первых двух?
Ответ. Только на 7.
Решение. Очевидно, что последняя цифра больше 1. Трёхзначное простое число не может оканчиваться ни на четную цифру (т. е. на 0, 2, 4, 6 или 8), ни на цифру 5. Если последняя цифра 3 или 9, то сумма всех цифр числа, равная удвоенной последней цифре, делится на 3, а тогда само число делится на 3. Таким образом, осталась только цифра семь.
Замечания. Есть четыре числа, удовлетворяющих условию задачи: 167, 257, 347, 527; приводить примеры таких чисел в решении не требовалось.

Задача 2. [4 балла]
Кролик, готовясь к приходу гостей, повесил в трёх углах своей многоугольной норы по лампочке. Пришедшие к нему Винни-Пух и Пятачок увидели, что не все горшочки с мёдом освещены. Когда они полезли за мёдом, две лампочки разбились. Кролик перевесил оставшуюся лампочку в некоторый угол так, что вся нора оказалась освещена. Могло ли такое быть? (Если да, нарисуйте пример, если нет, обоснуйте ответ.)
Ответ. Да, могло (см. рисунок).

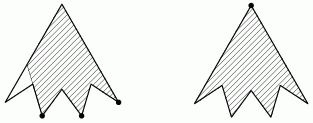
Замечание. Такое возможно, даже если заменить три на любое другое, сколь угодно большое число.

Задача 3. [4 балла]
На доске написаны три правильные несократимые дроби, дающие в сумме единицу, причем их числители - различные натуральные числа. Оказалось, что если каждую из этих дробей "перевернуть" (т. е. заменить на обратную), то сумма полученных дробей будет натуральным числом. Приведите пример таких дробей.
Ответ. Да, может. Например, 2/11, 3/11, 6/11.

Задача 4. [7 баллов]
Таня написала название своего родного города и все его циклические сдвиги, получив таблицу 1.
Затем, упорядочив эти "слова" по алфавиту, она составила таблицу 2 и выписала её последний столбец: ВКСАМО .

Таблица 1   Таблица 2

 МОСКВА      АМОСКВ
 АМОСКВ      ВАМОСК
 ВАМОСК      КВАМОС
 КВАМОС      МОСКВА
 СКВАМО      ОСКВАМ
 ОСКВАМ      СКВАМО

Г********О
К********С
Н********С
О********Н
О********Г
О********С
Р********О
С********Р
С********О
С********К

ГО*******О
КС*******С
НО*******С
ОГ*******Н
ОР*******Г
ОС*******С
РС*******О
СК*******Р
СН*******О
СО*******К

Задача 5. [6 баллов]
Сложите из фигур, изображенных на рисунке, квадрат размером 9*9 с вырезанным в его центре квадратом 3*3 (фигуры можно не только поворачивать, но и переворачивать).

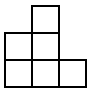
Ответ. См. задачу 4а шестого класса.

Задача 6. [8 баллов]
Из Цветочного города в Солнечный ведет шоссе длиной 12 км. На втором километре этого шоссе расположен железнодорожный переезд, который три минуты закрыт и три минуты открыт и т. д., а на четвёртом и на шестом километрах расположены светофоры, которые две минуты горят красным светом и три минуты - зеленым и т. д. Незнайка выезжает из Цветочного города в Солнечный в тот момент, когда переезд только что закрылся, а оба светофора только что переключились на красный. За какое наименьшее время (в минутах) он сможет доехать до Солнечного города, не нарушая правил, если его электромобиль едет по шоссе с постоянной скоростью (Незнайка не умеет ни тормозить, ни увеличивать скорость)?
Ответ. 24 мин.
Решение. Будем откладывать по оси абсцисс время (в минутах), а по оси ординат - расстояние от Цветочного города (в километрах). Так как скорость электромобиля постоянна, то график его движения - прямая. При этом Незнайка не может проезжать переезд, расположенный на втором километре шоссе, пока не истекут три минуты, а также на седьмой, восьмой и девятой минутах, на тринадцатой-пятнадцатой минутах и т. д. Графически это означает, что прямая не может пересекать выделенные отрезки.

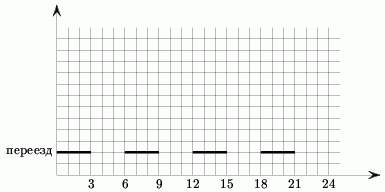
Аналогично можно отметить отрезки, которые запрещено пересекать из-за светофоров.

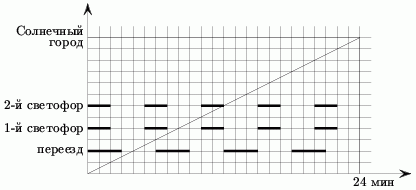
Осталось из начала координат провести прямую, которая не пересекает ни один из выделенных отрезков и пересекает горизонтальную прямую y=12 как можно раньше.

Дата последнего изменения — 15 февраля 2004 года