Задания | Результаты | Решения (doc-файл) | Решения (html-файл)
10
Первый тур (10 минут; каждая задача √ 6 баллов).
1.1. Известно, что числа а + b + c и ![]() являются целыми. Верно ли, что число
являются целыми. Верно ли, что число ![]() также является целым?
также является целым?
1.2. Есть четыре одинаковых кирпича размером ![]() . Объясните, как составить из них прямоугольный параллелепипед с наибольшей возможной длиной диагонали.
. Объясните, как составить из них прямоугольный параллелепипед с наибольшей возможной длиной диагонали.
1.3.
Найдите все натуральные значения n, при которых n5 + 2 делится на n + 2.Второй тур (15 минут; каждая задача √ 7 баллов
).
2.1.
Решите уравнение:2.2.
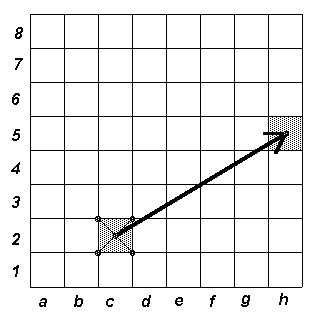
На шахматной доске построены векторы с началом в центре клетки С2 (см. рисунок) и концами в центрах всех остальных клеток. Найдите модуль суммы этих векторов, если сторона клетки доски равна 1.2.3.
Незнайка отметил на плоскости 15 точек и утверждает, что какое бы натуральное число N, где 1 £ N £ 7, ему ни назвали, он сможет указать прямую, содержащую ровно N отмеченных точек. Прав ли он?
Третий тур (15 минут; каждая задача √ 7 баллов
).3.1.
Последовательность чисел: 3; 7; 14; 24; ... такова, что разности соседних членов образуют арифметическую прогрессию. Найдите сотый член данной последовательности.3.2.
Диагонали трапеции АВСD (AD || BC) пересекаются в точке О. Докажите, что окружности, описанные около треугольников АОD и ВОС, касаются друг друга.3.3.
У Васи есть набор из 24 карандашей различных цветов. Он хочет раскрасить некоторое количество кругов по следующему правилу: каждый круг красится в три различных цвета, любое сочетание из двух цветов используется ровно один раз (то есть, если в каком-то круге встретились, например, красный и синий цвета, то ни в каком другом круге такое сочетание цветов невозможно) и каждое сочетание двух цветов должно быть использовано. Сможет ли он это сделать?Четвертый тур (20 минут; каждая задача √ 8 баллов
).4.1.
Решите уравнение:4.2.
Дан выпуклый четырехугольник ABCD. Известно, что равны радиусы окружностей, вписанных в треугольники ABC, ABD, ACD и BCD. Докажите, что АС = BD.4.3.
Каждое из первых 2004 простых чисел возвели в степень, равную этому числу. Затем перемножили полученные числа и прибавили единицу. Является ли полученное число точным квадратом?Пятый тур (25 минут; каждая задача √ 9 баллов
).5.1.
Известно, что x, y и z √ положительные числа, произведение которых равно 0,5. Докажите, что5.2.
М √ внутренняя точка отрезка АВ, длина которого 11 см. Рассматриваются всевозможные треугольники АВС. Найдите наименьшее возможное расстояние между центрами окружностей, описанных около треугольников САМ и СВМ.5.3.
На шахматной доске стоят десять белых фигур. Докажите, что можно поставить на эту доску черного коня так, чтобы он не нападал ни на одну из этих фигур.| Команда | 1|1 | 1|2 | 1|3 | 2|1 | 2|2 | 2|3 | 3|1 | 3|2 | 3|3 | 4|1 | 4|2 | 4|3 | 5|1 | 5|2 | 5|3 | сумма |
| 2 А (9 класс) | 6 | 6 | 4 | 5 | 0 | 7 | 7 | 7 | 0 | 8 | 8 | 8 | 0 | 9 | 9 | 84 (I) |
| СУНЦ_В | 6 | 6 | 3 | 5 | 0 | 7 | 7 | 7 | 7 | 2 | 8 | 8 | 0 | 9 | 8 | 83 (I) |
| 218 Г | 6 | 6 | 1 | 5 | 7 | 7 | 3 | 7 | 0 | 2 | 8 | 8 | 0 | 9 | 9 | 78 (II) |
| Сборная | 6 | 6 | 6 | 5 | 7 | 7 | 7 | 7 | 0 | 2 | 8 | 8 | 0 | 9 | 0 | 78 (II) |
| 82 А Черноголовка | 6 | 4 | 6 | 7 | 7 | 7 | 7 | 7 | 7 | 3 | 8 | 0 | 0 | 5 | 0 | 74 (II) |
| 57 (9 класс) | 6 | 4 | 6 | 7 | 5 | 7 | 5 | 7 | 7 | 2 | 0 | 0 | 0 | 9 | 7 | 72 (II) |
| 2 Д | 6 | 2 | 6 | 7 | 7 | 3 | 3 | 6 | 0 | 3 | 8 | 8 | 0 | 9 | 0 | 68 (III) |
| 1543 В | 6 | 2 | 6 | 5 | 7 | 7 | 0 | 7 | 0 | 3 | 8 | 0 | 0 | 9 | 7 | 67 (III) |
| 1101 А | 6 | 2 | 6 | 5 | 4 | 7 | 2 | 7 | 7 | 3 | 8 | 0 | 0 | 5 | 0 | 62 (III) |
| 2 Г | 6 | 2 | 0 | 7 | 0 | 7 | 7 | 7 | 0 | 2 | 8 | 0 | 0 | 9 | 1 | 56 (ПП) |
| 82 Б Черноголовка | 6 | 3 | 6 | 2 | 5 | 7 | 7 | 0 | 0 | 3 | 0 | 8 | 0 | 0 | 7 | 54 (ПП) |
| 1514 А | 6 | 1 | 0 | 5 | 0 | 7 | 7 | 0 | 7 | 8 | 8 | 0 | 0 | 5 | 0 | 54 (ПП) |
| 4 Б Королев | 6 | 4 | 3 | 5 | 7 | 7 | 0 | 0 | 0 | 6 | 8 | 0 | 0 | 7 | 0 | 53 (ПП) |
| СУНЦ_А | 6 | 6 | 1 | 1 | 7 | 1 | 1 | 7 | 0 | 0 | 8 | 3 | 0 | 9 | 3 | 53 (ПП) |
| 2 В | 6 | 2 | 0 | 1 | 4 | 0 | 7 | 7 | 0 | 8 | 0 | 8 | 0 | 9 | 0 | 52 (ПП) |
| 1543 А | 6 | 2 | 0 | 7 | 7 | 4 | 3 | 0 | 7 | 6 | 8 | 0 | 0 | 2 | 0 | 52 (ПП) |
| 218 А | 6 | 2 | 3 | 5 | 0 | 0 | 7 | 7 | 0 | 2 | 8 | 0 | 0 | 9 | 0 | 49 (ПП) |
| 1514 Б | 6 | 2 | 0 | 7 | 7 | 0 | 0 | 7 | 0 | 3 | 8 | 0 | 0 | 9 | 0 | 49 (ПП) |
| 218 Д | 6 | 0 | 6 | 0 | 0 | 7 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 9 | 4 | 46 |
| СУНЦ_Б | 6 | 4 | 3 | 1 | 0 | 0 | 7 | 0 | 0 | 2 | 0 | 8 | 0 | 5 | 9 | 45 |
| 4 А Королев | 6 | 2 | 4 | 5 | 0 | 7 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 9 | 7 | 43 |
| 218 Б | 6 | 2 | 1 | 0 | 2 | 4 | 3 | 0 | 7 | 0 | 8 | 0 | 0 | 9 | 0 | 42 |
| 1543 Г | 6 | 2 | 0 | 0 | 0 | 7 | 0 | 7 | 7 | 3 | 0 | 0 | 0 | 9 | 0 | 41 |
| 710 А | 6 | 2 | 6 | 5 | 5 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 40 |
| 1511 А | 6 | 6 | 6 | 7 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 7 | 40 |
| 152 Б | 6 | 5 | 6 | 1 | 0 | 3 | 7 | 0 | 6 | 2 | 0 | 0 | 0 | 2 | 0 | 38 |
| 1101 Б | 6 | 4 | 0 | 5 | 0 | 0 | 7 | 7 | 0 | 4 | 0 | 0 | 0 | 5 | 0 | 38 |
| 91 | 6 | 0 | 2 | 5 | 0 | 0 | 7 | 0 | 0 | 3 | 0 | 0 | 0 | 5 | 7 | 35 |
| 7 А | 6 | 3 | 6 | 0 | 0 | 7 | 0 | 0 | 7 | 8 | -1 | 0 | 0 | 0 | -2 | 34 |
| Троицк | 6 | 2 | 0 | 3 | 0 | 7 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 6 | 7 | 34 |
| 710 Б | 6 | 2 | 0 | 5 | 7 | 0 | 7 | 0 | 0 | 1 | 0 | 0 | 0 | 5 | 0 | 33 |
| 1189 А | 6 | 2 | 0 | 5 | 0 | 0 | 2 | 7 | 0 | 2 | 0 | 0 | 0 | 5 | 0 | 29 |
| 1511 Б | 6 | 4 | 2 | 1 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 29 |
| 4 Фрязино | 6 | 2 | 3 | 0 | 0 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 7 | 28 |
| 218 В | 6 | 2 | 3 | 1 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 4 | 28 |
| 1101 В | 5 | 2 | 0 | 0 | 0 | 3 | 7 | 0 | 0 | 3 | 0 | 0 | 0 | 1 | 0 | 21 |
| 345 | 6 | 2 | 0 | 3 | 0 | -1 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 18 |
| 2007 А | 6 | 2 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 2 | 0 | 16 |
| 7 Б | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 15 |
| 2007 Б | 6 | 2 | 2 | 0 | 0 | 0 | 3 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 15 |
| 1189 Б | 5 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 13 |
| 5 | 0 | 2 | 0 | 0 | 0 | -1 | 3 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 11 |
| 2007 Г | 6 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 10 |
| 2007 Д | 6 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 |
| 152 А | 0 | 2 | 0 | 2 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 |
| 2007 В | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 |
| 1101 Г | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 5 |
| "Алфавит" | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |