Математическая регата 10 классов 1.03.2008

1.1. Известно, что 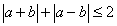. Докажите, что

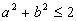
1.2. Найдите гипотенузу прямоугольного треугольника, если его сумма катетов равна 12, а сумма косинусов острых углов равна.

1.3. Можно ли разрезать куб на пять треугольных пирамид?

Второй тур (15 минут; каждая задача — 7 баллов).

2.1. Квадратный трехчлен f(x) = x² + аx + b имеет два корня, один из которых лежит внутри отрезка [0; 1], а другой – вне этого отрезка. Определите знак f(b).

2.2. На диагонали АС выпуклого четырехугольника АВСD выбрана точка О так, что OC = OD и РCОD = 90^o. Известно также, что РAОB = 110^o и точка О равноудалена от прямых DA, AB и BC. Найдите углы четырехугольника.

2.3. В верхнем углу таблицы 11ґ11 стоит число 1, а остальные клетки пусты. Сережа заполняет таблицу по следующему правилу: если в какой-то клетке стоит число x, то он ставит в любую соседнюю (по стороне) пустую клетку либо число 4x , либо число (x – 12), либо число (x + 3). Сможет ли он добиться того, чтобы сумма всех чисел таблицы стала равной нулю?

Третий тур (20 минут; каждая задача — 8 баллов).

3.1. Найдите наименьшее значение выражения (x + y)(x + z), где x, y и z – положительные числа и xyz(x + y + z) = 1.

3.2. Главные диагонали шестиугольного сечения куба пересекаются в одной точке. Обязательно ли это сечение проходит через центр куба?

3.3. Найдите все натуральные числа, которые в 11 раз больше суммы своих цифр.

4.1. Известно, что для положительных чисел а, b и c выполняется неравенство: . Докажите, что .

4.2. Вершина С прямого угла треугольника АВС лежит внутри окружности с центром О и радиусом R, проходящей через концы гипотенузы АВ, СН – высота треугольника АВС. На прямой АВ взята точка K так, что KН = ОН. Найдите СK.

4.3. При каких натуральных значениях n числа nⁿ + 1 и (2n)²ⁿ + 1 являются простыми одновременно?

Пятый тур (15 минут; каждая задача — 7 баллов).

5.1. Существует ли такая функция f(t), где tО [–1; 1], что для всех xО [0; p ] выполняется равенство f(cosx) = sinx?

5.2. Три высоты остроугольного треугольника пересекаются в точке H, которая делит одну из высот пополам, а другую в отношении 2 : 1, считая от вершины. В каком отношении точка H делит третью высоту?

5.3. На дискотеку пришло некоторое количество мальчиков и девочек, всего – не более 40 человек. Каждая девочка бросила взгляд на каждого знакомого мальчика, а каждый мальчик бросил взгляд на каждую незнакомую ему девочку. Всего было брошено 117 взглядов. Сколько мальчиков могло быть на этой дискотеке?