Математическая регата 10 классов 7.03.2009

1.1. Найдите значение выражения , если x² + y² = 6xy и x ¹ y.

1.2. При показе итогов регаты изображение вылезло за пределы квадратного экрана на 20 см (с каждой стороны). На какое наименьшее расстояние (выраженное целым количеством сантиметров) надо приблизить экран к проектору, чтобы изображение поместилось на экран полностью, если «угол зрения» проектора равен 60° ?

1.3. Кузнечик прыгает по координатной прямой. Сначала он прыгает из точки с координатой 0 в точку с координатой 1, а длина каждого следующего прыжка вдвое больше предыдущего. Сможет ли он вернуться в исходную точку, двигаясь подобным образом? (Направление каждого прыжка: влево или вправо – не зависит от направления предыдущего прыжка.)

Второй тур (15 минут; каждая задача — 7 баллов).

2.1. Решите систему уравнений: .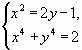

2.2. Найдите наибольший периметр параллелограмма, диагонали которого 6 см и 8 см.

2.3. В футбольном турнире участвовало 5 команд. Каждая команда сыграла с каждой по одному разу (выигрыш – 3 очка, ничья – 1 очко, проигрыш – 0). Все участники, кроме победителя, набрали очков поровну. Каков наименьший возможный отрыв команды-победителя?

Третий тур (20 минут; каждая задача — 8 баллов).

3.1. Изобразите такой график функции, определенной на отрезке [–4; 4], что при повороте на 90° с центром в начале координат он переходит в себя.

3.2. Биссектрисы углов треугольника АВС пересекают стороны ВС, СА и АВ в точках P, Q и R соответственно. Р₁ – точка пересечения прямой, проходящей через точку Р параллельно АВ, со стороной СА. Аналогично определяются точки Q₁ и R₁. Найдите сумму , если длины сторон исходного треугольника равны а, b и с.

3.3. Найдите все натуральные числа, которые можно представить в виде , где m и n – также натуральные числа.

Четвертый тур (25 минут; каждая задача — 9 баллов).

4.1. Пусть a_n – целое число, ближайшее к . Найдите все такие натуральные n, что .

4.2. На гипотенузе АВ равнобедренного прямоугольного треугольника АВС отмечены точки М и N так, что угол МСN равен 45° (точка M лежит между А и N). Докажите, что АМ² + BN² = MN².

4.3. Дано 51 различное натуральное число, меньшее 100. Докажите, что из них можно выбрать шесть таких чисел, что никакие два из выбранных не имеют одинаковых цифр ни в одном разряде.

Пятый тур (15 минут; каждая задача — 7 баллов).

5.1. Числа а, b, x и y удовлетворяют равенствам: (a + b)(x + y) = 1 и (a² + b²)(x² + y²) = 1. Докажите, что ax + by ³ 0.

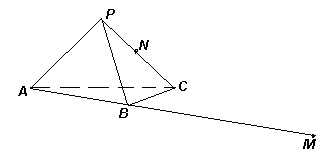
5.2. На столе стоит правильная треугольная пирамида РАВС (сделанная из стекла), все ребра которой равны 1 (см. рис.). Муравей ползет из точки М, лежащей на луче АВ на расстоянии 2 от точки В, в точку N – середину ребра РС. Найдите длину его кратчайшего пути.

5.3. Найдите все целые решения уравнения k(k + 1) = n³.

Результаты регаты: