10 класс.
Первый тур (10 минут; каждая задача — 6 баллов).
1.1. Решите уравнение: ![]() .
.
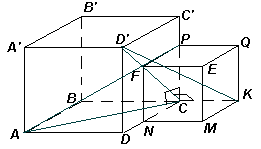
1.2. На плоскости АВС расположены два куба АВСDA’B’C’D’ и KMNCQEFP – так, как это показано на рисунке. Сравните длины отрезков AP и D’K.
1.3. Докажите, что сумма цифр в десятичной записи числа 3200 меньше, чем 1000.
Второй тур (15 минут; каждая задача — 7 баллов).
2.1. Известно, что а > b > c. Докажите, что ![]() .
.
2.2. В треугольнике АВС проведена биссектриса АL. Через точку L проведена прямая, перпендикулярная AL и пересекающая лучи АВ и АС в точках М и K соответственно. Найдите AK, если АВ = 4, АС = 6.
2.3. Какое наибольшее количество ладей можно расставить на шахматной доске так, чтобы любая белая ладья не била никакую ладью по горизонтали, а любая черная ладья не била никакую ладью по вертикали?
Третий тур (20 минут; каждая задача — 8 баллов).
3.1. Известно, что m2 + n2 = 1, k2 + p2 = 1 и mk + np = 0. Найдите mn + kp.
3.2. На сторонах ВС и CD квадрата ABCD произвольно выбраны точки Р и Q соответственно. Из вершины В на отрезки АР и АQ опущены перпендикуляры BB1 и BB2, а из вершины D – перпендикуляры DD1 и DD2 соответственно. Докажите, что отрезки B1B2 и D1D2 равны и перпендикулярны.
3.3. Полоска 1´ 100 разбита на единичные квадраты. В эти квадраты записывают числа 1, 2, ..., 100 следующим образом: сначала в какой-нибудь квадрат записывают число 1, затем в один из соседних квадратов записывают число 2, затем в один из соседних с уже занятыми квадратами записывают число 3, и так далее. Сколькими способами это можно проделать?
Четвертый тур (25 минут; каждая задача — 9 баллов).
4.1. Число а является корнем уравнения x3 – 3x2 + 5x – 17 = 0, а число b – корнем уравнения x3 – 3x2 + 5x + 11 = 0. Какие значения может принимать a + b?
4.2. Точка М – середина ребра АА1 треугольной призмы АBCA1B1C1. На прямой АВ1 выбрана точка Е, а на прямой ВС1 – точка F так, что прямые EF и СМ параллельны. Найдите ![]() .
.
4.3. Можно ли в десятичной записи числа А = 28999 изменить ровно одну цифру так, чтобы оно стало простым?
Пятый тур (15 минут; каждая задача — 7 баллов).
5.1. Известно, что уравнение x4 + px2 + q = 0 имеет ровно три корня. Сколько корней имеет уравнение x4 + qx2 + p = 0?
5.2. На боковых сторонах АВ и ВС равнобедренного треугольника АВС взяты точки Е и F соответственно. Отрезки ЕС и FА пересекаются в точке О. Докажите, что если площадь четырёхугольника ВЕОF равна площади треугольника АСО, то АЕ = ВF.
5.3. Существует ли выпуклый шестиугольник, у которого длина одной из сторон равна 1, а длины всех диагоналей – целые числа?
Результаты регаты:
|
Команда |
I тур |
II тур |
III тур |
IV тур |
V тур |
Сумма |
Диплом |
||||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|||
|
СУНЦ А |
6 |
6 |
6 |
7 |
7 |
7 |
8 |
8 |
8 |
9 |
0 |
9 |
7 |
7 |
7 |
102 |
I |
|
5А Долгопрудный |
6 |
6 |
6 |
7 |
7 |
7 |
0 |
8 |
8 |
0 |
5 |
9 |
7 |
7 |
7 |
90 |
II |
|
30А С-Петербург |
6 |
6 |
6 |
7 |
1 |
7 |
8 |
8 |
6 |
0 |
0 |
9 |
7 |
7 |
7 |
85 |
II |
|
2 В |
6 |
6 |
6 |
7 |
0 |
7 |
8 |
4 |
8 |
0 |
0 |
9 |
7 |
7 |
7 |
82 |
II |
|
Интеллектуал Б |
6 |
6 |
6 |
5 |
7 |
7 |
0 |
0 |
8 |
0 |
9 |
3 |
7 |
7 |
0 |
71 |
III |
|
СУНЦ В |
6 |
0 |
6 |
6 |
0 |
7 |
8 |
4 |
8 |
0 |
0 |
9 |
7 |
1 |
7 |
69 |
III |
|
1 1 8 9 А |
6 |
6 |
6 |
0 |
7 |
7 |
8 |
0 |
8 |
0 |
0 |
4 |
7 |
6 |
0 |
65 |
III |
|
1 5 1 4 Б |
1 |
6 |
6 |
7 |
7 |
7 |
0 |
4 |
8 |
0 |
0 |
3 |
7 |
7 |
0 |
63 |
III |
|
2 1 8 А |
0 |
6 |
6 |
7 |
0 |
7 |
4 |
8 |
8 |
0 |
0 |
9 |
7 |
0 |
0 |
62 |
III |
|
1 5 4 3 А |
6 |
0 |
6 |
7 |
7 |
7 |
8 |
1 |
0 |
5 |
9 |
3 |
0 |
0 |
0 |
59 |
ПП |
|
СУНЦ Б |
6 |
0 |
6 |
7 |
0 |
7 |
8 |
8 |
0 |
0 |
0 |
9 |
7 |
0 |
0 |
58 |
ПП |
|
1 3 0 3 А |
6 |
6 |
6 |
0 |
1 |
7 |
7 |
0 |
0 |
0 |
9 |
1 |
7 |
7 |
0 |
57 |
ПП |
|
1 5 1 4 А |
6 |
6 |
6 |
7 |
0 |
7 |
8 |
2 |
0 |
0 |
0 |
2 |
7 |
0 |
0 |
51 |
ПП |
|
3 1 5 Б |
0 |
5 |
6 |
7 |
2 |
7 |
0 |
4 |
0 |
0 |
9 |
1 |
0 |
7 |
0 |
48 |
ПП |
|
1 5 3 4 А |
6 |
6 |
6 |
0 |
1 |
0 |
0 |
1 |
2 |
0 |
0 |
9 |
7 |
7 |
0 |
45 |
ПП |
|
2 0 0 7 А |
6 |
6 |
6 |
5 |
0 |
2 |
8 |
0 |
0 |
0 |
0 |
7 |
5 |
0 |
45 |
ПП |
|
|
1 5 2 1 А |
6 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
8 |
9 |
0 |
9 |
6 |
0 |
0 |
44 |
ПП |
|
СУНЦ Г |
0 |
6 |
6 |
0 |
0 |
7 |
8 |
8 |
2 |
0 |
0 |
0 |
7 |
0 |
0 |
44 |
ПП |
|
5Б Долгопрудный |
0 |
6 |
6 |
6 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
3 |
7 |
7 |
7 |
43 |
ПП |
|
1 5 8 0 А |
6 |
6 |
6 |
5 |
0 |
3 |
1 |
7 |
0 |
0 |
0 |
3 |
6 |
0 |
0 |
43 |
ПП |
|
30Б С-Петербург |
6 |
6 |
6 |
7 |
7 |
0 |
0 |
0 |
8 |
0 |
0 |
2 |
0 |
0 |
0 |
42 |
ПП |
|
1 5 2 5 |
6 |
0 |
5 |
7 |
0 |
7 |
0 |
0 |
0 |
1 |
0 |
1 |
7 |
7 |
0 |
41 |
|
|
1 5 6 8 Б |
6 |
6 |
6 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
7 |
0 |
0 |
39 |
|
|
Кострома |
6 |
6 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
34 |
|
|
1 5 1 4 В |
6 |
6 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
0 |
33 |
|
|
1 5 6 8 Г |
6 |
6 |
6 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
32 |
|
|
2 0 0 7 Д |
1 |
6 |
6 |
7 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
3 |
7 |
0 |
0 |
32 |
|
|
5В Долгопрудный |
0 |
-1 |
1 |
7 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
0 |
28 |
|
|
9 1 Б |
6 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
7 |
7 |
0 |
28 |
|
|
2 0 0 7 Г |
6 |
6 |
6 |
0 |
1 |
0 |
8 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
28 |
|
|
1 5 6 4 А |
6 |
6 |
6 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
27 |
|
|
Переславль |
1 |
1 |
0 |
7 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
7 |
0 |
27 |
|
|
1 5 1 1 А |
6 |
6 |
6 |
0 |
-1 |
7 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
26 |
|
|
1 5 1 1 Б |
6 |
0 |
0 |
0 |
7 |
4 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
25 |
|
|
1 5 3 7 Б |
6 |
6 |
2 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
-1 |
0 |
7 |
2 |
0 |
25 |
|
|
2 1 8 В |
0 |
6 |
6 |
0 |
1 |
0 |
0 |
4 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
24 |
|
|
1 5 3 7 А |
1 |
0 |
0 |
7 |
0 |
2 |
8 |
0 |
2 |
0 |
0 |
1 |
0 |
3 |
0 |
24 |
|
|
1 5 8 0 В |
6 |
6 |
2 |
7 |
1 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
24 |
|
|
1 5 4 3 Б |
0 |
6 |
6 |
0 |
0 |
0 |
0 |
4 |
6 |
0 |
0 |
1 |
0 |
0 |
0 |
23 |
|
|
2 1 8 Б |
0 |
0 |
6 |
0 |
0 |
5 |
1 |
0 |
0 |
0 |
0 |
3 |
7 |
0 |
0 |
22 |
|
|
3 1 5 А |
1 |
0 |
2 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
9 |
4 |
0 |
7 |
0 |
22 |
|
|
3 1 5 В |
0 |
6 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
9 |
0 |
0 |
7 |
0 |
22 |
|
|
1 1 8 9 Б |
0 |
0 |
6 |
7 |
0 |
0 |
8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
22 |
|
|
1 9 2 А |
0 |
6 |
0 |
7 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
21 |
|
|
2 0 0 7 В |
6 |
0 |
0 |
7 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
21 |
|
|
5 4 Б |
0 |
5 |
4 |
7 |
0 |
2 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
20 |
|
|
9 1 А |
0 |
6 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
0 |
0 |
0 |
20 |
|
|
1 5 6 8 А |
6 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
7 |
0 |
0 |
20 |
|
|
1 9 2 Б |
0 |
5 |
4 |
7 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
19 |
|
|
1 1 0 6 |
6 |
0 |
0 |
0 |
0 |
2 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
|
|
2 1 8 Г |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
1 |
7 |
0 |
0 |
15 |
|
|
1 1 8 9 Г |
6 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
7 |
0 |
0 |
15 |
|
|
1 5 5 7 А |
0 |
6 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
14 |
|
|
7 |
6 |
0 |
6 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
13 |
|
|
1 5 6 8 В |
6 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
13 |
|||
|
1 5 8 0 Г |
0 |
6 |
3 |
0 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
13 |
|
|
1 3 0 3 Б |
0 |
6 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
4 |
0 |
0 |
0 |
12 |
|
|
1 5 6 4 В |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
3 |
0 |
12 |
|
|
1 5 3 7 В |
6 |
4 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
11 |
|
|
1 5 5 7 Б |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
7 |
2 |
0 |
10 |
|||||
|
5 4 В |
-1 |
0 |
0 |
0 |
7 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
||
|
9 1 В |
0 |
6 |
0 |
0 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
|
|
5 4 А |
1 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
|
|
1 5 8 1 А |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
8 |
|
|
6 5 4 А |
0 |
5 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
|
|
1 9 2 В |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
7 |
|||||||||
|
1 5 8 0 Б |
0 |
0 |
6 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
|
|
1 1 8 9 В |
1 |
0 |
3 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
|
|
1 5 6 4 Б |
1 |
0 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
6 |
|
|
1 5 8 1 Б |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
3 |
|
|
6 5 4 Б |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|||
|
1 4 2 5 А |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
||||
|
2 0 0 7 Б |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
1 4 2 5 Б |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||