Математическая регата 11 классов 14.11.2009

1.1. Касательная к графику y = x² пересекает координатные оси в точках А и В так, что ОА = ОВ. Найдите площадь треугольника АОВ.

1.2. Существует ли многогранник, у которого все грани – равнобокие трапеции?

1.3. Найдите все натуральные решения уравнения n² + 2n – n! = 0.

Второй тур (15 минут; каждая задача — 7 баллов).

2.1. Найдите все положительные решения системы уравнений .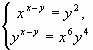

2.2. В параллелограмме АВСD диагональ АС вдвое больше стороны АВ. На стороне ВС выбрана точка K так, что Ð ADB = Ð KDB. В каком отношении точка K делит сторону ВС?

2.3. Найдите все тройки (p; q; r) простых чисел, для которых числа |p – q|, |q – r| и |r – p| также являются простыми.

Третий тур (20 минут; каждая задача — 8 баллов).

3.1. Вычислите , если .

3.2. В треугольнике АВС: R₁ и R₂ – радиусы окружностей, проходящих через вершину С и касающихся прямой АВ в точках А и В соответственно. Найдите радиус окружности, описанной около треугольника АВС.

3.3. В турнире по хоккею участвовало несколько команд. Каждая команда должна была сыграть с каждой по одному матчу. Но в ходе турнира ровно половина команд была дисквалифицирована и эти команды выбыли из турнира. В результате в турнире было сыграно 77 матчей. Оказалось, что все дисквалифицированные команды сыграли одинаковое количество матчей, причем они успели провести между собой все положенные встречи. Сколько команд было в турнире первоначально?

Четвертый тур (25 минут; каждая задача — 9 баллов).

4.1. Каждое из чисел а, b, c и d лежит на отрезке [2; 4]. Докажите, что выполняется неравенство: 25(ab + cd)² ³ 16(a² + d²)(b² + c²).

4.2. На плоскости заданы выпуклый n-угольник А₁А₂ ... A_n площади S и произвольная точка Р. Повернув точку Р на один и тот же заданный угол a относительно каждой из вершин данного многоугольника, получим новый n-угольник. Найдите его площадь.

4.3. Римский патриций решил устроить большой праздник и для этого приготовил 240 бочек вина. Однако к нему в подвал пробрался враг, который подсыпал яд в одну из бочек. У патриция есть 5 драгоценных камней со следующим свойством: если камень окунуть в отравленное вино, то он почернеет в течение часа (в какой момент – неизвестно). До праздника осталось ровно два часа. Патриций готов пожертвовать камнями, чтобы найти отравленную бочку. Объясните, каким образом это можно сделать.

Пятый тур (15 минут; каждая задача — 7 баллов).

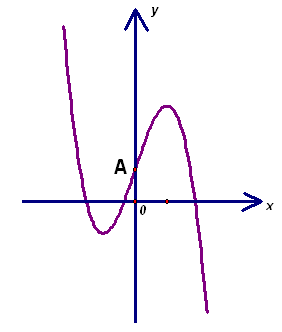
5.1. Точка А – центр симметрии графика функции f(x)= ах³ + bх² + сх + d (см. рисунок). Сравните коэффициенты а, b, с и d с нулем.

5.2. В четырехугольнике АВСD диагональ BD является биссектрисой угла АВС, Е – точка пересечения диагоналей, AD = DC, Ð ADC = 140° , Ð BEC = 110° . Найдите угол АСВ.

5.3. Существует ли 2009-значное натуральное число N, для которого число M = N^N + (N + 1)^N + 1 является составным?

Результаты регаты: