9 класс
Первый тур (10 минут; каждая задача – 6 баллов)
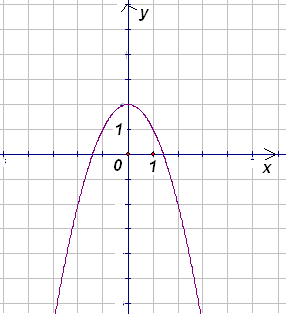
1.1. На координатной плоскости изображен график функции y = ax2 + c (см. рисунок). В каких точках график функции y = cx + a пересекает оси координат?
1.2. В равнобокой трапеции AВСD основания AD и ВС равны 12 и 6 соответственно, а высота равна 4. Сравните углы ВАС и САD.
1.3. На доске записаны числа 1, 21, 22, 23, 24, 25. Разрешается стереть любые два числа и вместо них записать их разность – неотрицательное число. Может ли на доске в результате нескольких таких операций остаться только число 15?
Второй тур (15 минут; каждая задача – 7 баллов)
2.1. Известно, что 5(а – 1) = b + a2. Сравните числа а и b.
2.2. В остроугольном треугольнике АВС угол В равен 45° , АМ и CN – его высоты, О – центр описанной окружности, Н – ортоцентр (точка пересечения высот). Докажите, что ОNHМ – параллелограмм.
2.3. Найдите наименьшее натуральное n, при котором число А = n3 + 12n2 + 15n + 180 делится на 23.
Третий тур (20 минут; каждая задача – 8 баллов)
3.1. Пятеро друзей скинулись на покупку. Могло ли оказаться так, что любые два из них внесли менее одной трети общей стоимости?
3.2. Существует ли прямоугольный треугольник, в котором две медианы перпендикулярны?
3.3. Какое наибольшее суммарное количество белых и черных шашек можно расставить в клетках доски 8´ 8 так, чтобы выполнялось следующее условие: в каждой горизонтали и в каждой вертикали белых шашек должно быть в два раза больше, чем черных?
Четвертый тур (25 минут; каждая задача – 9 баллов)
4.1. Для различных положительных чисел а и b выполняется равенство ![]() =
= ![]() . Докажите, что а и b – взаимно обратные числа.
. Докажите, что а и b – взаимно обратные числа.
4.2. В выпуклом четырехугольнике ABCD: Ð ВАС = 20° , Ð ВСА = 35° , Ð ВDС = 40° , Ð ВDА = 70° . Найдите угол между диагоналями четырехугольника.
4.3. Найдите все простые числа p, q и r, для которых выполняется равенство: p + q = (p – q)r.
Пятый тур (15 минут; каждая задача – 7 баллов)
5.1. Найдите наибольшее натуральное n такое, что n200 < 5300.
5.2. В трапеции ABCD биссектриса тупого угла B пересекает основание AD в точке K – его середине, M – середина BC, AB = BC. Найдите отношение KM : BD.
5.3. Существует ли натуральное число, которое при делении на сумму своих цифр как в частном, так и в остатке дает число 2011?