11 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Найдите ближайшее целое число к числу x, если x = : 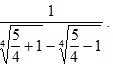
1.2. В параллелограмме АВСD точка Е – середина стороны AD, точка F – основание перпендикуляра, опущенного из вершины В на прямую СЕ. Найдите площадь треугольника ABF, если АВ = а, ∠ВАF = α.
1.3. Натуральные числа A и B делятся на все натуральные числа от 1 до 65. На какое наименьшее натуральное число может не делиться число A + B?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. У многочленов Р(х) и Q(х) – один и тот же набор целых коэффициентов (их порядок – различен). Докажите, что разность Р(2015) – Q(2015) кратна 1007.
2.2. Около единичного квадрата ABCD описана окружность, на которой выбрана точка М. Какое наибольшее значение может принимать произведение MA·MB·MC·MD?
2.3. Решите в натуральных числах уравнение: x3 + y3 + 1 = 3xy.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Решите уравнение: 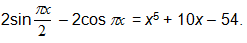
3.2. На сторонах BC и AC правильного треугольника ABC отмечены точки X и Y соответственно. Докажите, что из отрезков AX, BY и XY можно составить треугольник.
3.3. На плоскости проведены n прямых так, что любые две пересекаются, но никакие 4 через одну точку не проходят. Всего имеются 16 точек пересечения, причем через 6 из них проходят по 3 прямые. Найдите n.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Алгебраисты придумали новую операцию ❆, которая удовлетворяет условиям: а ❆ а = 0 и а ❆ (b ❆ c) = (a ❆ b) + c. Вычислите 2015 ❆ 2014. (Знак «+» определяет сложение в обычном смысле, скобки показывают порядок действий.)
4.2. Четырехугольник АВСD вписан в окружность, I – центр окружности, вписанной в треугольник ABD. Найдите наименьшее значение BD, если AI = BC = CD = 2.
4.3. У натурального числа n есть такие два различных делителя а и b, что (а – 1)(b + 2) = n – 2. Докажите, что число 2n является квадратом натурального числа.
Пятый тур (15 минут; каждая задача – 7 баллов).