9 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Известно, что значения выражений  и
и  находится в интервале (–0,9; –0,8). В каком интервале лежат значения выражения
находится в интервале (–0,9; –0,8). В каком интервале лежат значения выражения 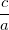 ?
?
1.2. Верно ли, что любой треугольник можно разбить на 4 равнобедренных треугольника?
1.3. Верно ли, что любое положительное четное число можно представить в виде произведения целых чисел, сумма которых равна нулю?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Решите уравнение: 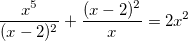 .
.
2.2. В равнобедренном треугольнике АВС с основанием ВС проведена биссектриса CL. Докажите, что CL < 2BL.
2.3. Существует ли прямоугольный треугольник, у которого длины двух сторон – целые числа, а длина третьей стороны равна 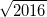 ?
?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. По кольцевой дорожке длиной 60 см движутся в обе стороны муравьи со скоростью 1 см/c. Когда два муравья сталкиваются, они мгновенно разворачиваются и движутся с той же скоростью в противоположных направлениях. Оказалось, что за минуту произошло 48 попарных столкновений. Сколько муравьев могло быть на дорожке?
3.2. Пусть СН – высота остроугольного треугольника АВС, О – центр описанной около него окружности. Точка Т – проекция вершины С на прямую АО. В каком отношении прямая ТН делит сторону ВС? Сколько муравьев могло быть на дорожке?
3.3. Дано 100 целых чисел. Из первого числа вычли сумму цифр второго числа, из второго вычли сумму цифр третьего числа, и так далее, наконец, из 100-го числа вычли сумму цифр первого числа. Могут ли эти разности оказаться соответственно равными 1, 2, … , 100 в каком-то порядке?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Решите систему уравнений: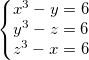 .
.
4.2. Внутри равностороннего треугольника ABC отмечена точка M так, что ∠AMC = 150°. Докажите, что отрезки АМ, ВМ и СМ таковы, что сумма квадратов двух из них равна квадрату третьего.
4.3. На столе лежит прямоугольный лист бумаги. Саша разрезает его по прямой на две части и кладёт части на стол. Потом он берёт одну из частей, снова режет по прямой на две части и кладёт части обратно на стол. Потом снова берёт со стола и разрезает одну часть, и так далее. Какое наименьшее количество разрезов необходимо сделать Саше, чтобы на столе оказалось, по крайней мере, 252 одиннадцатиугольника?
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. График линейной функции у = kх + k + 1, где k > 0, пересекает оси координат в точках А и В. Какова наименьшая возможная площадь треугольника АВО (О – начало координат)?
5.2. Две окружности касаются друг друга в точке C и прямой l в точках A и B. Прямая ВC пересекает вторую окружность в точке D. Докажите, что угол BАD – прямой.
5.3. Дано 10 натуральных чисел. Из десяти всевозможных сумм по 9 чисел всего 9 различных: 86, 87, 88, 89, 90, 91, 93, 94, 95. Найдите исходные числа.
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | 5 тур | Сумма | Диплом | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| Г М К А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 0 | 7 | 7 | 5 | 100 | I |
| 2 Б | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 0 | 8 | 0 | 5 | 7 | 7 | 90 | I |
| 2 А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 1 | 0 | 0 | 7 | 7 | 7 | 85 | I |
| 1 7 9 В | 6 | 0 | 6 | 7 | 7 | 7 | 0 | 0 | 8 | 9 | 0 | 0 | 3 | 7 | 7 | 67 | II |
| Г М К Б | 0 | 0 | 6 | 1 | 7 | 7 | 1 | 8 | 8 | 1 | 0 | 9 | 7 | 7 | 5 | 67 | II |
| 2 0 0 7 А | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 4 | 0 | 0 | 0 | 0 | 7 | 7 | 7 | 64 | II |
| 1 5 6 8 В | 6 | 6 | 6 | 7 | 0 | 7 | 1 | 8 | 8 | 1 | 0 | 2 | 2 | 7 | 0 | 61 | II |
| 2 0 0 7 В | 6 | 0 | 6 | 1 | 0 | 7 | 1 | 1 | 8 | 9 | 0 | 0 | 7 | 7 | 7 | 60 | II |
| 2 В | 6 | 0 | 0 | 7 | 0 | 7 | 1 | 8 | 4 | 0 | 0 | 3 | 7 | 7 | 2 | 52 | III |
| 1 5 1 4 А | 6 | 6 | 6 | 7 | 0 | 0 | 8 | 0 | 8 | 1 | 0 | 3 | 7 | 0 | 0 | 52 | III |
| 1 7 9 А | 6 | 5 | 6 | 0 | 7 | 0 | 1 | 8 | 8 | 1 | 9 | 0 | 0 | 0 | 0 | 51 | III |
| 1 5 4 3 А | 6 | 6 | 6 | 7 | 0 | 7 | 8 | 1 | 0 | 1 | 0 | 0 | 1 | 7 | 0 | 50 | III |
| 4 4 4 А | 6 | 0 | 0 | 7 | 0 | 7 | 8 | 1 | 0 | 0 | 0 | 0 | 7 | 7 | 5 | 48 | III |
| ЛНИП А Королёв | 6 | 5 | 6 | 0 | 0 | 7 | 0 | 8 | 0 | 1 | 0 | 3 | 0 | 7 | 4 | 47 | III |
| 1 7 9 Б | 6 | 6 | 0 | 6 | 7 | 4 | 0 | 8 | 0 | 1 | 0 | 0 | 0 | 7 | 0 | 45 | III |
| 2 0 0 7 Б | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 0 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 43 | |
| 1 5 3 4 Б | 6 | 0 | 6 | 7 | 0 | 7 | 0 | 0 | -1 | 9 | 0 | 0 | 1 | 0 | 7 | 42 | |
| 8 5 3 Б | 6 | 3 | 6 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 3 | 7 | 7 | 0 | 40 | |
| 1 5 1 4 Б | 6 | 6 | 0 | 0 | 0 | 7 | 6 | 0 | 0 | 1 | 0 | 0 | 7 | 7 | 0 | 40 | |
| 5 А Долгопр. | 0 | 0 | 6 | 1 | 0 | 7 | 8 | 1 | 8 | 1 | 0 | 0 | 0 | 7 | 0 | 39 | |
| 1 5 8 0 | 6 | 0 | 0 | 0 | 7 | 7 | 0 | 0 | 8 | 0 | 9 | 0 | 0 | 0 | 0 | 37 | |
| ЦДО 9 | 6 | 0 | 6 | 0 | 0 | 7 | 8 | 0 | 0 | 1 | 9 | 0 | 0 | 0 | 0 | 37 | |
| 2 Г | 0 | 3 | 6 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 6 | 0 | 36 | |
| 2 0 0 7 Г | 6 | 3 | 6 | 1 | 7 | 0 | 0 | 8 | 0 | 1 | 0 | 3 | 1 | 0 | 0 | 36 | |
| Курчатовская А | 0 | 0 | 6 | 7 | 0 | 0 | 1 | 0 | 4 | 1 | 0 | 3 | 5 | 7 | 0 | 34 | |
| ЛНИП Б Королёв | 6 | 0 | 6 | 7 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 3 | 1 | 0 | 0 | 31 | |
| 1 5 6 8 А | 1 | 0 | 6 | 7 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 7 | 0 | 30 | |
| Раменское | 0 | 0 | 6 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 2 | 29 | |
| 30 СПб | 6 | 0 | 6 | 7 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 7 | 0 | 0 | 28 | |
| 1 5 3 4 В | 0 | 6 | 6 | 7 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 3 | 3 | 0 | 0 | 27 | |
| 1 5 3 4 А | 0 | 0 | 6 | 7 | 0 | 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 26 | |
| 1 5 3 7 А | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 7 | 3 | 0 | 25 | |
| 1 5 6 8 Б | 0 | 0 | 6 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 0 | 7 | 0 | 24 | |
| Г С Г | 6 | 0 | 6 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 7 | 0 | 0 | 24 | |
| 1 5 8 1 Б | 6 | 3 | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 23 | |
| 5 4 8 | 0 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 0 | 22 | |
| 1 2 0 8 | 1 | 0 | 0 | 7 | 7 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 22 | |
| Г М К В | 0 | 0 | 0 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 21 | |
| 5 Б Долгопр. | 0 | 3 | 2 | 0 | 7 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 20 | |
| 5 В Долгопр. | 6 | 0 | 6 | 0 | 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 20 | |
| 1 9 2 Б | 6 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 20 | |
| 1 5 1 1 А | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 0 | 0 | 19 | |
| Курчатовская Б | 6 | 3 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 19 | |
| 2 1 8 А | 6 | 0 | 0 | 7 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 18 | |
| Курчатовская Г | 0 | 0 | 6 | 0 | 0 | 7 | 0 | 1 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 18 | |
| 1 5 6 8 Г | 0 | 0 | 6 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 17 | |
| Алексин | 4 | 0 | 0 | 0 | 5 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 17 | |
| 8 7 9 | 0 | 2 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 1 | 0 | 3 | 1 | 0 | 0 | 15 | |
| 8 2 0 | 0 | 0 | 0 | 7 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | |
| Подольск | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 14 | |
| 4 4 4 Б | 0 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | |
| 1 9 2 А | 1 | 0 | 0 | 0 | 7 | 0 | 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 12 | |
| 1 5 1 1 Б | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 0 | 6 | 0 | 12 | |
| 2 1 0 1 Б | 0 | 3 | 0 | 0 | 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | |
| Курчатовская В | 0 | 0 | 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 10 | |
| 8 5 3 А | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 8 | |
| 8 5 3 В | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 7 | 0 | 8 | |
| Н Г Ш | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 0 | 8 | |
| 1 5 8 1 А | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 2 1 0 1 А | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 1 6 7 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | |
| 2 1 8 Б | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 0 | 0 | 0 | 6 | |
| 1 4 3 4 А | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 5 | |
| 1 4 3 4 Б | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | |
| 1 5 3 3 Б | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | |
| 9 4 9 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | |
| 1 5 3 7 Б | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 5 3 3 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 4 6 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 9 4 9 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 3 9 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Снегири | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |