8 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Про числа a, b и c известно, что (a + b)2 + (b + c)2 + (a + c)2 = (a + b + c)2. Какие значения могут принимать a, b и c?
1.2. Существует ли многоугольник с попарно различными сторонами, из которого после одного перегибания получается квадрат?
1.3. Найдите разность между наибольшим и наименьшим трехзначными числами, у каждого из которых совпадают частное и остаток при делении на 51.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. При каком натуральном значении n значение выражения 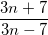 будет наименьшим?
будет наименьшим?
2.2. На стороне AC равнобедренного треугольника ABC (AB = AC) отметили точку Е. На отрезке АЕ отложили отрезок ЕD = ВЕ. Найдите угол DBC, если известно, что ∠CBE = ∠DBA .
2.3. Какое наибольшее количество месяцев, содержащих по пять пятниц, может быть в одном году?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Электричка Москва – Петушки проходит начальный путь – от Курского вокзала до Дрезны – втрое дольше, чем от Леоново до Петушков. При этом на путь от Дрезны до Петушков у нее уходит в два раза меньше времени, чем от Курского вокзала до Леоново. Во сколько раз время пути от Курского вокзала до Петушков больше, чем от Дрезны до Леоново?
3.2. На стороне BC равностороннего треугольника ABC отмечена точка M, а на продолжении стороны AC за точку C – точка N, причем AM = MN. Докажите, что BM = CN.
3.3. В каждой клетке таблицы 2019×2019 записали число 1 или число –1. Затем подсчитали произведения в каждой строке и в каждом столбце. Могла ли сумма всех полученных произведений оказаться равной 2020?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. На доске были записаны четыре положительных числа. Каждый из шести школьников выбрал два из них и перемножил. В итоге все получили различные результаты, при этом у пяти школьников они были равны 2, 3, 4, 5 и 6. Найдите результат шестого школьника и докажите, что описанная ситуация возможна.
4.2. Дан параллелограмм ABCD, отличный от ромба. Вписанные окружности треугольников ABC и ADC касаются диагонали AC в точках X и Y. Вписанные окружности треугольников BCD и BAD касаются диагонали BD в точках Z и T. Докажите, что точки X, Y, Z и T являются вершинами прямоугольника.
4.3. При каких значениях n можно расположить по кругу n > 3 попарно различных натуральных чисел так, чтобы каждое число было равно либо наибольшему общему делителю, либо наименьшему общему кратному двух своих соседей?
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | Сумма | Диплом | ||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| 1 5 1 4 А | 6 | 6 | 6 | 6 | 7 | 7 | 8 | 8 | 8 | 1 | 9 | 9 | 81 | I |
| 1 3 2 9 А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 5 | 0 | 9 | 77 | I |
| Летово А | 6 | 6 | 6 | 7 | 7 | 2 | 8 | 8 | 8 | 5 | 0 | 7 | 70 | II |
| 2 0 0 7 А | 6 | 6 | 6 | 0 | 7 | 7 | 8 | 8 | 8 | 5 | 4 | 4 | 69 | II |
| 1 5 3 4 Г | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 0 | 8 | 5 | 9 | 0 | 69 | II |
| 1 7 9 А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 0 | 4 | 0 | 67 | II |
| 1 7 9 Б | 6 | 6 | 6 | 7 | 7 | 4 | 8 | 8 | 8 | 5 | 0 | 2 | 67 | II |
| 1 3 2 9 Б | 6 | 6 | 6 | 7 | 7 | 2 | 8 | 8 | 8 | 0 | 4 | 2 | 64 | III |
| 2 Б | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 0 | 8 | 0 | 4 | 4 | 63 | III |
| 2 В | 6 | 6 | 6 | 7 | 7 | 4 | 8 | 8 | 8 | 0 | 0 | 2 | 62 | III |
| 1 5 4 3 А | 6 | 0 | 6 | 7 | 7 | 4 | 8 | 8 | 0 | 5 | 9 | 2 | 62 | III |
| 1 5 1 4 В | 6 | 6 | 6 | 7 | 0 | 0 | 8 | 8 | 8 | 0 | 4 | 8 | 61 | III |
| Интеллектуал Б | 6 | 6 | 6 | 7 | 7 | 5 | 0 | 8 | 7 | 0 | 0 | 9 | 61 | III |
| Летово Г | 6 | 0 | 6 | 7 | 0 | 7 | 8 | 8 | 0 | 0 | 9 | 9 | 60 | III |
| 1 5 6 8 В | 6 | 0 | 0 | 7 | 7 | 7 | 8 | 8 | 8 | 0 | 0 | 9 | 60 | III |
| 1 5 1 4 Б | 6 | 6 | 4 | 7 | 3 | 0 | 8 | 8 | 8 | 0 | 0 | 9 | 59 | III |
| 4 4 4 А | 6 | 6 | 6 | 7 | 7 | 2 | 8 | 0 | 8 | 0 | 9 | 0 | 59 | III |
| 5 4 8 В | 6 | 6 | 6 | 7 | 7 | 6 | 8 | 0 | 7 | 0 | 4 | 0 | 57 | ПП |
| 1 5 5 7 А | 6 | 6 | 4 | 7 | 7 | 4 | 8 | 0 | 8 | 5 | 0 | 1 | 56 | ПП |
| 5 А Долгопрудный | 6 | 0 | 6 | 7 | 7 | 0 | 8 | 8 | 8 | 0 | 0 | 5 | 55 | |
| 1 5 3 4 А | 6 | 6 | 6 | 7 | 7 | 0 | 0 | 8 | 8 | 0 | 0 | 7 | 55 | |
| Черноголовка | 6 | 6 | 6 | 7 | 7 | 0 | 8 | 1 | 8 | 0 | 4 | 0 | 53 | |
| 5 4 Г | 6 | 6 | 0 | 7 | 7 | 0 | 8 | 0 | 8 | 0 | 0 | 7 | 49 | |
| 1 5 3 4 В | 6 | 6 | 5 | 7 | 0 | 0 | 8 | 0 | 8 | 0 | 0 | 9 | 49 | |
| ЛНИП В Королёв | 6 | 4 | 0 | 7 | 7 | 0 | 8 | 8 | 0 | 0 | 4 | 4 | 48 | |
| 5 7 | 6 | 6 | 6 | 7 | 7 | 0 | 8 | 0 | 7 | 0 | 0 | 0 | 47 | |
| Нижний Новгород | 3 | 4 | 6 | 7 | 7 | 0 | 8 | 8 | 0 | 0 | 4 | 0 | 47 | |
| 1 5 6 8 Б | 6 | 6 | 6 | 7 | 7 | 2 | 8 | 0 | 0 | 0 | 4 | 0 | 46 | |
| 1 5 1 4 Г | 6 | 6 | 6 | 0 | 7 | 4 | 8 | 0 | 8 | 0 | 0 | 0 | 45 | |
| 2 Г | 6 | 6 | 0 | 7 | 7 | 2 | 8 | 0 | 8 | 0 | 0 | 0 | 44 | |
| 3 0 А С.-Петербург | 6 | 6 | 0 | 7 | 7 | 4 | 8 | 0 | 0 | 0 | 4 | 2 | 44 | |
| 1 5 6 8 Г | 6 | 6 | 6 | 6 | 7 | 0 | 0 | 0 | 8 | 0 | 4 | 1 | 44 | |
| 2 0 0 7 Б | 6 | 0 | 6 | 7 | 0 | 4 | 8 | 0 | 8 | 0 | 4 | 0 | 43 | |
| Летово Б | 6 | 0 | 4 | 7 | 7 | 4 | 8 | 0 | 0 | 0 | 0 | 4 | 40 | |
| 1 5 8 1 Б | 6 | 6 | 6 | 7 | 0 | 4 | 1 | 0 | 8 | 0 | 0 | 2 | 40 | |
| 2 0 8 6 Б | 1 | 6 | 5 | 0 | 7 | 4 | 8 | 8 | 0 | 0 | 0 | 0 | 39 | |
| 5 4 8 А | 6 | 6 | 0 | 7 | 7 | 0 | 0 | 0 | 8 | 5 | 0 | 0 | 39 | |
| 1 5 1 1 А | 6 | 6 | 6 | 1 | 0 | 0 | 7 | 0 | 8 | 0 | 4 | 0 | 38 | |
| Воронеж | 6 | 0 | 6 | 7 | 7 | 0 | 0 | 8 | 0 | 0 | 4 | 0 | 38 | |
| 2 0 0 7 Г | 6 | 6 | 6 | 7 | 7 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 36 | |
| 2 0 8 6 А | 6 | 0 | 4 | 7 | 7 | 0 | 0 | 0 | 8 | 0 | 4 | 0 | 36 | |
| 5 Б Долгопрудный | 6 | 0 | 6 | 7 | 7 | 4 | 0 | 0 | 0 | 0 | 4 | 1 | 35 | |
| 1 5 6 8 А | 6 | 0 | 6 | 7 | 7 | 0 | 0 | 0 | 7 | 0 | 0 | 2 | 35 | |
| 3 0 Б С.-Петербург | 6 | 6 | 6 | 7 | 0 | 0 | 1 | 8 | 0 | 0 | 0 | 0 | 34 | |
| 5 4 А | 6 | 6 | 6 | 7 | 1 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 34 | |
| 1 5 4 3 Б | 6 | 6 | 5 | 4 | 7 | -1 | 0 | 8 | -1 | 0 | 0 | 0 | 34 | |
| 4 4 4 Б | 1 | 6 | 0 | 7 | 0 | 0 | 8 | 8 | 0 | 0 | 4 | 0 | 34 | |
| 5 4 В | 6 | 6 | 0 | 7 | 7 | -1 | 0 | 8 | 0 | 0 | 0 | 0 | 33 | |
| Курчатовская Б | 6 | 6 | 6 | 7 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 33 | |
| Летово В | 6 | 6 | 6 | 0 | 7 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 33 | |
| Тверь | 6 | 0 | 6 | 0 | 5 | -1 | 8 | 8 | 0 | 0 | 0 | 1 | 33 | |
| 1 5 1 1 Б | 6 | 6 | 6 | 0 | 0 | 0 | 8 | 0 | 6 | 0 | 0 | 0 | 32 | |
| 1 5 3 4 Б | 4 | 6 | 4 | 6 | 0 | 0 | 0 | 8 | -1 | 0 | 4 | 1 | 32 | |
| 2 А | 6 | 0 | 6 | 0 | 7 | 0 | 0 | 1 | 0 | 5 | 4 | 0 | 29 | |
| 2 1 8 Б | 6 | 0 | 4 | 7 | 0 | 4 | 8 | 0 | 0 | 0 | 0 | 0 | 29 | |
| 4 4 4 В | 6 | 6 | 6 | 0 | 7 | 1 | 1 | 0 | 0 | 0 | 0 | 2 | 29 | |
| 1 2 7 3 А | 6 | 0 | 6 | 7 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 2 | 29 | |
| ЛНИП Б Королёв | 6 | 0 | 0 | 7 | 7 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 28 | |
| 2 1 0 1 А | 6 | 0 | 6 | 7 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 27 | |
| 2 1 8 А | 6 | 0 | 6 | 7 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 27 | |
| Снегири | 6 | 0 | 6 | 7 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 27 | |
| 2 1 0 1 В | 6 | 6 | 6 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | |
| 2 1 0 7 | 6 | 0 | 4 | 7 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 25 | |
| Курчатовская А | 6 | 6 | 0 | 1 | 0 | 0 | 8 | 0 | 0 | 0 | 4 | 0 | 25 | |
| 1 2 7 3 Б | 6 | 0 | 4 | 7 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 25 | |
| ЛНИП А Королёв | 6 | 6 | 0 | 0 | 1 | 4 | 4 | 0 | 0 | 0 | 0 | 2 | 23 | |
| 5 4 Б | 0 | 6 | 0 | 6 | 1 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 21 | |
| 9 4 9 | 0 | 0 | 5 | 7 | 0 | 1 | 8 | 0 | 0 | 0 | 0 | 0 | 21 | |
| 2 0 0 7 В | 6 | 0 | 6 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 20 | |
| Курчатовская В | 6 | 0 | 5 | 1 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 20 | |
| 5 4 8 Б | 6 | 0 | 6 | 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 20 | |
| 2 1 0 1 Б | 1 | 0 | 0 | 7 | 1 | 0 | 8 | 0 | 0 | 0 | 2 | 0 | 19 | |
| Интеллектуал А | 6 | 0 | 0 | 6 | 0 | 2 | 1 | 0 | 0 | 0 | 4 | 0 | 19 | |
| 1 5 8 0 | 6 | 0 | 0 | 7 | 7 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 19 | |
| 1 5 5 7 Г | 0 | 0 | 0 | 7 | 0 | 2 | 8 | 0 | 0 | 0 | 0 | 0 | 17 | |
| 1 3 А Королёв | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 15 | |
| 1 5 1 7 В | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | |
| 1 9 9 5 Б | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 4 | 0 | 12 | |
| 1 3 Б Королёв | 4 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | |
| 1 5 5 7 В | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 8 | |
| 1 5 1 7 Б | 6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 1 5 5 7 Б | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 1 5 8 1 А | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| Дмитров 4 А | 0 | 0 | 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 4 6 3 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 1 9 9 5 В | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | |
| 1 5 1 7 А | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | |
| 1 9 9 5 А | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| Дмитров 4 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |