10 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите неравенство: 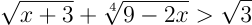
1.2. При каких значениях n > 2 можно разбить произвольный треугольник на n трапеций?
1.3. Можно ли расставить по кругу числа 0, 1, 2, ..., 9 так, чтобы сумма любых трёх чисел, стоящих подряд, была меньше 15?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Известно, что числа 2a + b, 2b + c и 2c + a являются членами бесконечной в обе стороны арифметической прогрессии. Верно ли, что число 5a – 2b также является членом этой прогрессии?
2.2. N > 2 прямых, проходящих через фиксированную точку, делят плоскость на 2N равных углов. Из произвольной точки плоскости, не принадлежащей ни одной из данных прямых, опущены перпендикуляры на эти прямые. Докажите, что основания перпендикуляров являются вершинами правильного многоугольника.
2.3. В каждой клетке таблицы размером 3x3 записано натуральное число так, что среди шести их сумм по строкам и по столбцам нет равных (сами числа не обязательно различные). Какое наименьшее значение суммы всех чисел в этой таблице?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Решите систему уравнений: 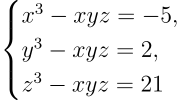
3.2. Из точки А проведена к окружности касательная АВ и секущая АС (точки В и С лежат на окружности). D – вторая точка пересечения АС с окружностью (см. рисунок), М – середина АВ. Отрезок СМ пересекает окружность в точке K. Найдите угол МАK, если ∠DСK = 18°.
3.3. На окружности отмечено n точек. Рассматриваются все тройки отрезков с концами в отмеченных точках, в которых каждые два отрезка имеют общую точку (внутреннюю, либо один из концов). Сколько всего таких троек?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Решите уравнение: sin15x = 15sinx.
4.2. Равнобедренные треугольники АВС и A'B'C' лежат в параллельных плоскостях так, что точка С' равноудалена от вершин треугольника АВС, а точки A' и B' удалены на такое же расстояние от прямых, содержащих стороны этого треугольника. Найдите отношение площадей треугольников A'B'C' и АВС.
4.3. Верно ли, что в любом бесконечном множестве, состоящем из натуральных чисел, найдутся три различных числа, сумма двух из которых делится на третье?
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Решите уравнение: 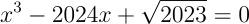
5.2. На стороне АВ квадрата АВСD отмечена точка Е. Расстояния от вершин В и D до прямой СЕ равны m и n. Найдите длину стороны квадрата.
5.3. Про натуральные числа m и n известно, что m ≥ n и НОK(m; n) = 75НОД(m; n). Докажите, что m ≥ 8n.
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | 5 тур | Сумма | Диплом | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| Л 2 Ш А | 6 | 6 | 0 | 7 | 7 | 7 | 5 | 8 | 4 | 9 | 0 | 9 | 7 | 7 | 7 | 89 | I |
| 5 А Долгопрудный | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 4 | 2 | 0 | 1 | 7 | 7 | 7 | 83 | I |
| Л 2 Ш В | 6 | 6 | 1 | 7 | 7 | 7 | 5 | 8 | 8 | 0 | 1 | 3 | 7 | 7 | 7 | 80 | II |
| Ш Ц П М А | 6 | 0 | 6 | 7 | 3 | 7 | 0 | 8 | 0 | 9 | 0 | 9 | 7 | 7 | 7 | 76 | II |
| 4 4 4 Б | 6 | 6 | 0 | 7 | 7 | 7 | 0 | 8 | 8 | 1 | 1 | 1 | 7 | 7 | 7 | 73 | III |
| 2 0 0 7 М | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 8 | 0 | 1 | 0 | 9 | 1 | 7 | 7 | 72 | III |
| 5 В Долгопрудный | 6 | 6 | 6 | 7 | 7 | 3 | 0 | 8 | 0 | 3 | 0 | 1 | 7 | 7 | 7 | 68 | III |
| 1 5 1 1 В | 6 | 0 | 6 | 7 | 7 | 7 | 8 | 8 | 4 | 0 | 0 | 0 | 2 | 7 | 5 | 67 | III |
| Л 2 Ш Б | 6 | 6 | 7 | 7 | 7 | 0 | 8 | 0 | 3 | 1 | 9 | 6 | 0 | 7 | 67 | III | |
| Летово Б | 0 | 6 | 0 | 7 | 7 | 7 | 0 | 8 | 8 | 1 | 1 | 0 | 7 | 7 | 7 | 66 | III |
| Чуйкова А | 0 | 6 | 0 | 7 | 7 | 7 | 0 | 8 | 8 | 1 | 0 | 1 | 7 | 7 | 7 | 66 | III |
| 1 7 9 Г | 6 | 6 | 6 | 2 | 7 | 3 | 0 | 8 | 4 | 1 | 1 | 4 | 7 | 0 | 7 | 62 | ПП |
| 3 8 А Н.Новгород | 6 | 0 | 0 | 7 | 7 | 7 | 0 | 8 | 4 | 1 | 0 | 0 | 7 | 7 | 7 | 61 | ПП |
| 1 7 9 В | 0 | 6 | 0 | 7 | 7 | 7 | 0 | 8 | 1 | 0 | 0 | 1 | 7 | 7 | 7 | 58 | ПП |
| 1 7 9 Е | 6 | 5 | 0 | 7 | 7 | 3 | 4 | 0 | 4 | 1 | 0 | 0 | 7 | 7 | 7 | 58 | ПП |
| 1 7 9 Б | 0 | 5 | 6 | 7 | 7 | 7 | 0 | 0 | 3 | 1 | 0 | 8 | 7 | 1 | 5 | 57 | ПП |
| 4 4 4 А | 6 | 6 | 0 | 7 | 7 | 7 | 0 | 8 | 0 | 1 | 0 | 7 | 0 | 7 | 56 | ПП | |
| Ф Т Ш В СПб | 6 | 6 | 0 | 7 | 7 | 7 | 0 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | 56 | ПП |
| Ш Ц П М В | 6 | 0 | 0 | 7 | 7 | 3 | 0 | 8 | 3 | 0 | 1 | 0 | 7 | 7 | 7 | 56 | ПП |
| 5 4 8 В | 0 | 6 | 6 | 7 | 3 | 7 | 0 | 1 | 1 | 3 | 0 | 0 | 7 | 7 | 7 | 55 | ПП |
| 1 5 4 3 Б | 0 | 0 | 6 | 0 | 7 | 7 | 0 | 0 | 0 | 5 | 8 | 7 | 7 | 7 | 54 | ПП | |
| 2 0 8 6 Б | 0 | 6 | 0 | 7 | 0 | 7 | 0 | 0 | 0 | 4 | 0 | 8 | 7 | 7 | 7 | 53 | ПП |
| 1 5 3 4 Е | 0 | 1 | 0 | 7 | 0 | 7 | 0 | 1 | 6 | 4 | 0 | 5 | 7 | 7 | 7 | 52 | |
| 1 7 1 В | 6 | 6 | 0 | 7 | 7 | 7 | 0 | 1 | 0 | 1 | 1 | 1 | 7 | 0 | 7 | 51 | |
| 5 Г Долгопрудный | 6 | 6 | 0 | 0 | 7 | 0 | 4 | 8 | 4 | 1 | 0 | 0 | 7 | 0 | 7 | 50 | |
| 4 4 4 Г | 6 | 0 | 6 | 7 | 0 | 7 | 0 | 8 | 1 | 0 | 0 | 7 | 0 | 7 | 49 | ||
| Летово Г | 6 | 1 | 0 | 7 | 3 | 7 | 0 | 1 | 0 | 2 | 0 | 0 | 7 | 7 | 7 | 48 | |
| 2 0 0 7 О | 0 | 2 | 0 | 0 | 7 | 7 | 0 | 0 | 4 | 9 | 0 | 0 | 7 | 7 | 4 | 47 | |
| 5 Б Долгопрудный | 6 | 0 | 0 | 7 | 7 | 7 | 0 | 1 | 1 | 2 | 0 | 0 | 7 | 7 | 0 | 45 | |
| 2 0 0 7 Л | 0 | 6 | 0 | 7 | 7 | 7 | 0 | 0 | 0 | 3 | 1 | 0 | 7 | 0 | 7 | 45 | |
| Ш Ц П М Г | 0 | 0 | 6 | 7 | 0 | 7 | 0 | 8 | 1 | 0 | 0 | 0 | 7 | 7 | 0 | 43 | |
| 1 5 3 5 А | 0 | 6 | 6 | 0 | 4 | 0 | 0 | 0 | 0 | 1 | 4 | 0 | 7 | 7 | 7 | 42 | |
| 5 7 Г | 6 | 0 | 0 | 7 | 0 | 3 | 0 | 0 | 2 | 1 | 0 | 0 | 7 | 7 | 7 | 40 | |
| Летово А | 0 | 0 | 6 | 7 | 3 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 7 | 7 | 7 | 39 | |
| В Ш Э Е | 6 | 0 | 0 | 7 | 0 | 7 | 4 | 1 | 0 | 5 | 0 | 0 | 2 | 6 | 0 | 38 | |
| 1 5 1 1 Б | 0 | 0 | 0 | 7 | 0 | 7 | 0 | 8 | 0 | 1 | 0 | 0 | 7 | 0 | 7 | 37 | |
| В Ш Э В | 6 | 6 | 0 | 7 | 0 | 1 | 0 | 1 | 8 | 1 | 0 | 0 | 7 | 0 | 0 | 37 | |
| 3 1 5 Г | 0 | 6 | 6 | 7 | 0 | 7 | 0 | 0 | 0 | 3 | 0 | 7 | 0 | 0 | 36 | ||
| 8 6 А Ярославль | 0 | 0 | 6 | 7 | 3 | 7 | 0 | 1 | 1 | 1 | 0 | 0 | 4 | 5 | 35 | ||
| 2 0 9 8 М | 0 | 6 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 7 | 7 | 7 | 35 | |
| 5 7 В | 0 | 6 | 6 | 3 | 3 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 7 | 0 | 5 | 34 | |
| 1 7 1 Г | 0 | 1 | 0 | 7 | 3 | 3 | 0 | 0 | 0 | 5 | 0 | 0 | 7 | 7 | 0 | 33 | |
| 1 5 8 0 Б | 0 | 6 | 0 | 0 | 0 | 7 | 0 | 0 | 1 | 5 | 0 | 0 | 0 | 7 | 7 | 33 | |
| 4 4 4 В | 0 | 2 | 0 | 0 | 0 | 7 | 0 | 1 | 0 | 1 | 0 | 0 | 7 | 7 | 7 | 32 | |
| 5 4 8 Б | 1 | 6 | 0 | 0 | 0 | 7 | 0 | 7 | 0 | 3 | 1 | 0 | 0 | 0 | 7 | 32 | |
| 1 7 1 А | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 1 | 1 | 2 | 0 | 0 | 7 | 0 | 7 | 31 | |
| Ф Т Ш А СПб | 0 | 0 | 0 | 7 | 3 | 7 | 0 | 1 | 0 | 5 | 0 | 0 | 0 | 7 | 0 | 30 | |
| 1 5 1 1 А | 0 | 0 | 0 | 7 | 0 | 3 | 0 | 0 | 0 | 3 | 0 | 0 | 7 | 7 | 2 | 29 | |
| Ш Ц П М Д | 6 | 1 | 3 | 7 | 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 28 | |
| В Ш Э Г | 0 | 0 | 0 | 7 | 0 | 7 | 0 | 0 | 2 | 3 | 0 | 0 | 0 | 0 | 7 | 26 | |
| 1 5 8 0 Г | 6 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 7 | 2 | 23 | ||
| Летово В | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 7 | 0 | 0 | 23 | |
| 1 3 5 А Самара | 0 | 6 | 0 | 0 | 0 | 7 | 0 | 0 | 1 | 0 | 0 | 0 | 7 | 0 | 0 | 21 | |
| 2 1 0 1 А | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 7 | 7 | 18 | |
| 1 7 1 Д | 0 | 1 | 0 | 7 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 16 | |
| 1 5 8 0 Д | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | 5 | 15 | |
| 1 5 8 0 В | 1 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 7 | 0 | 14 | |
| 2 0 0 7 И | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 13 | ||
| 1 5 3 4 В | 1 | 0 | 0 | 0 | 3 | 7 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 12 | |||
| 4 4 В Липецк | 0 | 1 | 1 | 0 | 0 | 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 11 | |
| 1 6 3 6 Б | 0 | 0 | 0 | 7 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | |
| 2 5 А Кострома | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 9 | |
| 1 2 9 6 А | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 8 | ||||
| 2 2 4 В | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 1 4 1 1 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 2 | 4 | |
| 2 2 4 Б | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| 1 3 7 0 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 1 0 1 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 2 0 1 Б | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | |
| 1 6 3 6 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | -1 | -2 | |