9 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Какое наименьшее натуральное число надо прибавить к сумме 313 + 913, чтобы получить квадрат натурального числа?
1.2. В прямоугольном треугольнике ABC с прямым углом C проведена медиана AM. Может ли выполняться равенство AB = 2AM?
1.3. Решите в целых числах систему уравнений: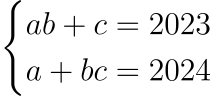
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Для положительных чисел a и b выполняется неравенство a – b > 4. Докажите, что тогда выполняется неравенство 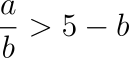 .
.
2.2. Через точку А окружности с центром О проведена касательная, а через точку В, также лежащую на окружности, проведен луч ОВ, пересекающий эту касательную в точке Е. Из точки А опущен перпендикуляр АС на ОВ, а из точки В – перпендикуляр BD на АЕ. Докажите, что ВС = BD.
2.3. На острове проживает 2024 жителя, каждый из которых либо рыцарь (который всегда говорит правду), либо лжец (который всегда лжёт). Однажды все жители острова разбились на пары, и каждый сказал: «Он – рыцарь!» либо «Он – лжец!» про своего соседа по паре. Оказалось, что тех и других фраз произнесено поровну. Какое наименьшее количество лжецов может жить на острове?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Сколько отрицательных корней имеет уравнение: x4 – 5x3 – 4x2 – 7x + 4 = 0?
3.2. В треугольнике АВС отрезки АМ и СР являются биссектрисами углов А и С соответственно, причём АР + СМ = АС. Найдите величину угла В.
3.3. На доске записаны в ряд квадраты натуральных чисел в возрастающем порядке так, что разность любых двух соседних чисел – простое число или квадрат простого числа. Какое наибольшее количество чисел может быть записано?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Известно, что для положительных x, y и z выполняются равенства: xy = z + a, yz = x + a, zx = y + a. Какие значения может принимать a?
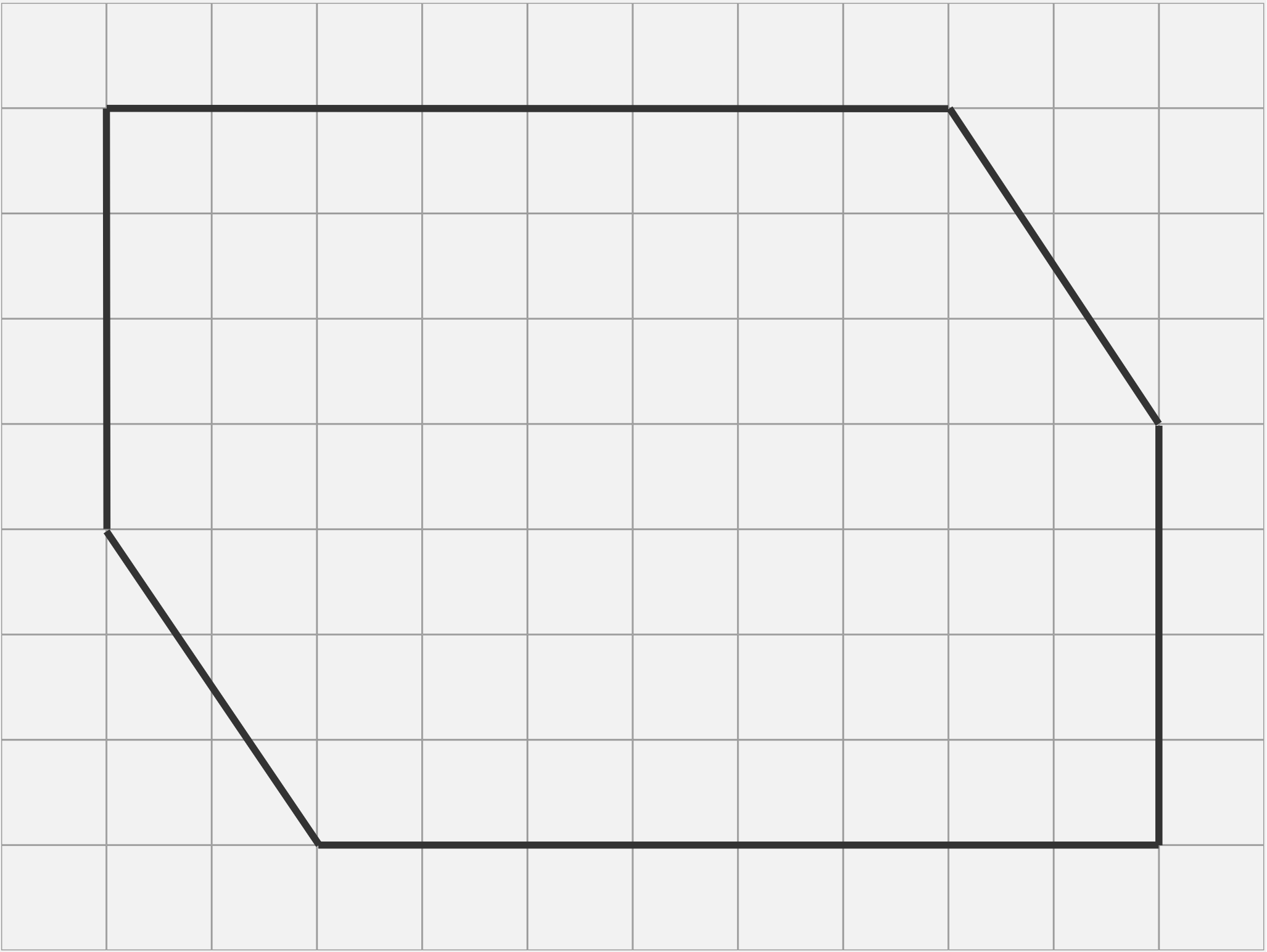
4.2. От прямоугольника со сторонами 7 и 10 клеток отрезали два прямоугольных треугольника с катетами 2 и 3 клетки (см. рисунок). Разрежьте получившийся шестиугольник на две части и сложите из них квадрат.
4.3. На конференцию приехали 200 учёных. Двое из них знают по 21 участнику конференции, ещё двое – по 22, ещё двое – по 23 и так далее, а последние двое – по 120. Может ли оказаться, что их можно посадить в два актовых зала так, чтобы в каждом зале были только незнакомые друг с другом?
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Разложите на множители, каждый из которых имеет степень не выше двух: x4 + y4 + (x + y)4.
5.2. Существует ли треугольник, в котором окружность, построенная на стороне как на диаметре, касается окружности, проходящей через середины его сторон?
5.3. Существует ли десятизначное число, кратное 7, все цифры в десятичной записи которого различны?
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | 5 тур | Сумма | Диплом | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| Летово К | 3 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 7 | 7 | 7 | 108 | I |
| Л 2 Ш О | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 4 | 9 | 9 | 9 | 7 | 7 | 7 | 107 | I |
| 2 0 0 7 Г | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 5 | 9 | 9 | 9 | 0 | 7 | 7 | 101 | II |
| В Г А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 3 | 5 | 9 | 5 | 7 | 7 | 7 | 98 | II |
| 1 7 9 В | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 0 | 0 | 7 | 7 | 95 | II |
| 2 0 0 7 З | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 0 | 0 | 7 | 7 | 95 | II |
| Л 2 Ш К | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 0 | 7 | 0 | 7 | 95 | II |
| 1 7 9 Г | 6 | 6 | 5 | 0 | 0 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 7 | 5 | 7 | 94 | II |
| Л 2 Ш Е | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 8 | 8 | 9 | 9 | 0 | 7 | 7 | 7 | 94 | II |
| Чуйкова Г | 6 | 6 | 3 | 7 | 7 | 7 | 8 | 1 | 8 | 5 | 9 | 9 | 4 | 7 | 7 | 94 | II |
| 2 0 8 6 Б | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 0 | 0 | 0 | 7 | 88 | III |
| Л 2 Ш Г | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 7 | 9 | 0 | 7 | 0 | 7 | 0 | 85 | III |
| Летово И | 6 | 6 | 0 | 7 | 7 | 7 | 0 | 8 | 8 | 3 | 0 | 9 | 7 | 7 | 7 | 82 | III |
| 1 7 9 А | 6 | 6 | 5 | 7 | 7 | 7 | 7 | 3 | 8 | 9 | 9 | 0 | 0 | 0 | 7 | 81 | III |
| Ю М Ш В | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 1 | 2 | 8 | 0 | 9 | 0 | 7 | 7 | 81 | III |
| Ф Т Ш В | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 1 | 8 | 9 | 0 | 0 | 0 | 7 | 7 | 79 | III |
| Ф Т Ш Г | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 8 | 8 | 9 | 0 | 0 | 0 | 7 | 7 | 78 | III |
| Ф Т Ш Б | 6 | 6 | 6 | 7 | 7 | 0 | 8 | 7 | 8 | 9 | 0 | 0 | 0 | 5 | 7 | 76 | ПП |
| Ю М Ш А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 1 | 4 | 9 | 9 | 1 | 0 | 5 | 0 | 76 | ПП |
| Школково А | 6 | 6 | 6 | 7 | 0 | 7 | 8 | 8 | 8 | 5 | 0 | 0 | 0 | 5 | 7 | 73 | ПП |
| 1 7 9 Б | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 4 | 5 | 8 | 0 | 0 | 0 | 0 | 72 | ПП |
| 3 1 5 Д | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 1 | 8 | 0 | 0 | 0 | 7 | 0 | 7 | 70 | ПП |
| 2 0 0 7 Ж | 6 | 6 | 0 | 7 | 7 | 7 | 0 | 8 | 2 | 9 | 0 | 9 | 0 | 7 | 0 | 68 | |
| В Г Б | 6 | 6 | 3 | 5 | 7 | 7 | 0 | 0 | 8 | 3 | 0 | 9 | 0 | 7 | 7 | 68 | |
| 4 0 Н. Новгород | 6 | 6 | 1 | 7 | 7 | 7 | 0 | 8 | 2 | 4 | 9 | 9 | 0 | 0 | 0 | 66 | |
| Ф Т Ш И | 3 | 6 | 2 | 7 | 7 | 7 | 8 | 0 | 2 | 9 | 0 | 0 | 0 | 7 | 7 | 65 | |
| 1 5 6 8 Ж | 6 | 6 | 6 | 7 | 7 | 7 | 4 | 1 | 8 | 0 | 0 | 9 | 0 | 0 | 0 | 61 | |
| 2 0 0 7 Р | 6 | 6 | 6 | 0 | 7 | 7 | 8 | 0 | 0 | 9 | 0 | 5 | 0 | 0 | 7 | 61 | |
| 5 4 8 В | 6 | 6 | 6 | 7 | 0 | 7 | 0 | 0 | 2 | 9 | 9 | 0 | 0 | 7 | 0 | 59 | |
| Ю М Ш Д | 6 | 6 | 3 | 7 | 7 | 4 | 0 | 1 | 2 | 5 | 0 | 9 | 0 | 0 | 7 | 57 | |
| 1 5 1 4 Е | 1 | 6 | 3 | 6 | 7 | 7 | 8 | 8 | 1 | 9 | 0 | 0 | 0 | 0 | 0 | 56 | |
| В Г В | 6 | 6 | 6 | 7 | 7 | 6 | 6 | 0 | -1 | 5 | 0 | 1 | 0 | 0 | 7 | 56 | |
| Сигма А | 6 | 6 | 0 | 7 | 0 | 7 | 8 | 1 | 3 | 5 | 0 | 5 | 0 | 0 | 7 | 55 | |
| 4 4 4 Е | 0 | 6 | 3 | 7 | 7 | 7 | 0 | 0 | 2 | 9 | 0 | 5 | 0 | 5 | 0 | 51 | |
| 1 7 1 А | 3 | 6 | 6 | 0 | 7 | 7 | 8 | 1 | 0 | 3 | 0 | 8 | 0 | 0 | 0 | 49 | |
| 5 8 Б | 3 | 6 | 0 | 7 | 7 | 7 | 0 | 1 | -1 | 3 | 0 | 0 | 7 | 7 | 0 | 47 | |
| Л Н И П Г | 0 | 6 | 6 | 7 | 0 | 7 | -1 | 5 | 4 | 5 | 0 | 0 | 0 | 7 | 0 | 46 | |
| 1 5 5 7 И | 6 | 6 | 6 | 0 | 7 | 7 | 8 | 0 | 2 | 0 | 0 | 3 | 0 | 0 | 0 | 45 | |
| Летово Ж | 0 | 6 | 3 | 7 | 7 | 7 | 0 | 8 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 42 | |
| Ю М Ш Б | 5 | 6 | 3 | 7 | 0 | 7 | 0 | 3 | -1 | 5 | 0 | 0 | 0 | 7 | 0 | 42 | |
| 9 Белгород Г | 0 | 6 | 6 | 7 | 0 | 7 | 0 | 1 | -1 | 5 | 0 | 3 | 0 | 0 | 7 | 41 | |
| 1 5 1 4 К | 0 | 5 | 3 | 7 | 7 | 7 | 0 | 1 | 4 | 3 | 0 | 0 | 0 | 0 | 0 | 37 | |
| 1 5 3 7 В | 0 | 0 | 4 | 7 | 7 | 7 | 4 | 1 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 33 | |
| 1 5 3 7 Г | 3 | 6 | 3 | 3 | 0 | 5 | 8 | 1 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 32 | |
| Примакова А | 6 | 4 | 2 | 7 | 0 | 7 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 30 | |
| Т Г У Б | 0 | 0 | 3 | 0 | 7 | 3 | 0 | 1 | 0 | 0 | 9 | 0 | 0 | 0 | 7 | 30 | |
| 2 0 0 9 З | 0 | 0 | 3 | 7 | 0 | 7 | 0 | 1 | 2 | 0 | 9 | 0 | 0 | 0 | 0 | 29 | |
| Примакова Б | 4 | 6 | 0 | 0 | 0 | 5 | 8 | 1 | -1 | 0 | 0 | 0 | 0 | 5 | 0 | 28 | |
| 1 5 5 7 К | 0 | 6 | 0 | 0 | 7 | 4 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 7 | 26 | |
| И Т Ш А | 3 | 6 | 0 | 7 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 5 | 0 | 25 | |
| 1 5 8 1 В | 0 | 6 | 3 | 0 | 0 | 5 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 19 | |
| 1 3 6 3 В | 0 | 0 | 0 | 0 | 7 | 5 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 17 | |
| 1 9 9 Г | 0 | 6 | 0 | 0 | 7 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | |
| 1 3 6 3 Б | 3 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 7 | 16 | |
| 1 3 5 5 Ж | 0 | 6 | 0 | 0 | 0 | 0 | 0 | -1 | 2 | 0 | 0 | 1 | 0 | 0 | 7 | 15 | |
| Т Г У В | 0 | 0 | 0 | 0 | 7 | 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | |
| 1 0 8 0 Б | 0 | 6 | 0 | 0 | 0 | 4 | 0 | 1 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 14 | |
| Т Г У А | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 14 | |
| 5 0 4 В | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 13 | |
| 2 0 0 9 Д | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 2 | 3 | 0 | 1 | 0 | 0 | 0 | 13 | |
| НИУ В Ш Э Е | 0 | 0 | 0 | 0 | 0 | 7 | 0 | -1 | 1 | 0 | 0 | 1 | 0 | 5 | 0 | 13 | |
| Покровский Г | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 13 | |
| 7 2 7 В | 4 | 3 | 0 | 0 | 0 | 1 | -1 | 1 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 11 | |
| 1 5 5 2 В | 0 | 0 | 0 | 0 | 6 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | |
| 1 4 9 9 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 7 | |
| 1 7 4 1 А | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 1 3 5 5 Е | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | |
| 2 0 0 9 Г | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | |
| 1 3 6 3 Д | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| 2 0 0 9 Ж | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | |
| 1 3 8 3 А | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 9 3 7 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 1 5 5 В | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | |
| 1 3 5 5 З | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Покровский Б | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | |