10 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Сравните: 20252025 + 20242024 и 20252024 + 20242025.
1.2. Существует ли четырёхугольник, у которого сумма диагоналей меньше любой его стороны?
1.3. Может ли сумма квадратов трёх последовательных натуральных чисел оказаться равной 20000025?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Решите уравнение: 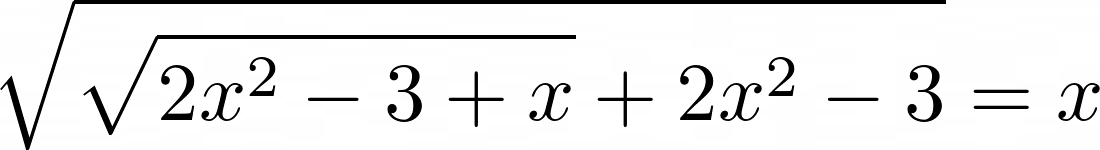
2.2. Окружность с центром в точке пересечения диагоналей АС и ВD равнобедренной трапеции ABCD касается меньшего основания ВС и боковой стороны АВ. Найдите площадь трапеции ABCD, если известно, что ее высота равна 16, а радиус окружности равен 3.
2.3. Имеется куб размером 10×10×10, состоящий из маленьких единичных кубиков. В центре O одного из угловых кубиков сидит кузнечик. Он может прыгать в центр любого кубика, имеющего общую грань с тем, в котором кузнечик находится в данный момент, причём так, чтобы расстояние до точки O увеличивалось. Сколькими способами кузнечик сможет допрыгать до углового кубика, противоположного исходному?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. На координатной плоскости постройте множество точек, удовлетворяющих неравенству y2 + y ≥ |x| + x – 1.
3.2. Окружность, вписанную в равнобедренный треугольник, перенесли параллельно его основанию на расстояние, равное её радиусу. Докажите, что в таком положении она касается окружности, описанной около данного треугольника.
3.3. На клетчатой плоскости отмечены 100 узлов, не лежащие на одной прямой. Докажите, что из них можно выбрать два узла X и Y, не лежащие на одной линии сетки, так, чтобы прямоугольник с диагональю XY и сторонами, параллельными линиям сетки, содержал не менее, чем 20 отмеченных узлов.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Пусть а, b и с – такие действительные числа, отличные от нуля, что (ab + bc + ca)3 = abc(a + b + c)3. Докажите, что а, b и с в некотором порядке образуют геометрическую прогрессию.
4.2. В тетраэдре ABCD грани АВС и ADC перпендикулярны, АВ = ВС = CD, BD = AC. Найдите угол между плоскостями АВD и ACD.
4.3. Хромая ладья ходит на соседнюю по стороне клетку. Пусть количество способов обойти всю шахматную доску хромой ладьёй (побывав на каждой клетке ровно по одному разу), если начало пути в клетке a1, равно A. Количество способов аналогично обойти всю шахматную доску хромой ладьёй, если начало пути в клетке b2, равно B. Докажите, что A > B.
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Пусть P(x) – квадратный трехчлен. Верно ли, что всегда можно найти такой многочлен четвертой степени Q(x), что уравнение P(Q(x)) = 0 не имеет действительных корней?
5.2. М – точка пересечения медиан прямоугольного треугольника АВС с прямым углом С. Может ли угол АМВ быть не больше, чем 135°?
5.3. Найдите остаток от деления 3105 + 5100 на 28.
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | 5 тур | Сумма | Диплом | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| 1 7 9 А | 6 | 6 | 6 | 0 | 2 | 7 | 8 | 8 | 3 | 9 | 1 | 9 | 7 | 7 | 7 | 86 | I |
| 2 0 0 7 Б | 6 | 6 | 6 | 0 | 6 | 7 | 8 | 0 | 8 | 9 | 0 | 9 | 7 | 7 | 7 | 86 | I |
| 2 0 0 7 В | 6 | 6 | 6 | 0 | 0 | 7 | 4 | 8 | 8 | 1 | 9 | 9 | 7 | 7 | 7 | 85 | I |
| Ф Т Л И Долгопр. | 5 | 6 | 6 | 2 | 4 | 7 | 8 | 8 | 8 | 9 | 0 | 0 | 7 | 7 | 7 | 84 | I |
| 1 7 9 Г | 6 | 6 | 6 | 7 | 2 | 7 | 8 | 8 | 8 | 0 | 0 | 9 | 0 | 7 | 7 | 81 | II |
| Л 2 Ш В | 6 | 6 | 6 | 0 | 0 | 7 | 8 | 0 | 8 | 9 | 0 | 9 | 7 | 7 | 7 | 80 | II |
| 1 7 9 Б | 6 | 6 | 6 | 0 | 6 | 7 | 6 | 0 | 8 | 0 | 0 | 9 | 7 | 7 | 7 | 75 | II |
| Чуйкова А | 6 | 6 | 6 | 4 | 0 | 7 | 8 | 0 | 8 | 9 | 0 | 6 | 7 | 7 | 1 | 75 | II |
| 2 ? 2 А | 6 | 6 | 6 | 0 | 5 | 7 | 4 | 8 | 0 | 9 | 0 | 9 | 7 | 0 | 7 | 74 | II |
| Л 2 Ш Б | 6 | 0 | 6 | 0 | 2 | 7 | 8 | 8 | 8 | 0 | 0 | 9 | 6 | 7 | 7 | 74 | II |
| Летово Б | 6 | 6 | 6 | 7 | 6 | 7 | 3 | 0 | 8 | 1 | 0 | 9 | 7 | 0 | 7 | 73 | III |
| Ф Т Л А Долгопр. | 6 | 6 | 6 | 7 | 5 | 6 | 4 | 0 | 0 | 5 | 0 | 6 | 7 | 7 | 7 | 72 | III |
| Летово В | 6 | 6 | 6 | 0 | 0 | 7 | 2 | 8 | 6 | 0 | 9 | 0 | 7 | 7 | 7 | 71 | III |
| Ф М Ш Б Тюмень | 6 | 6 | 6 | 0 | 5 | 7 | 2 | 8 | 8 | 0 | 0 | 2 | 7 | 7 | 7 | 71 | III |
| К Э П Л В Киров | 6 | 6 | 6 | 0 | 0 | 6 | 1 | 8 | 8 | 8 | 0 | 0 | 7 | 7 | 7 | 70 | III |
| 1 7 9 В | 0 | 0 | 7 | 8 | 8 | 8 | 6 | 1 | 9 | 7 | 7 | 7 | 68 | III | |||
| 3 1 5 В | 6 | 6 | 6 | 3 | 0 | 7 | 8 | 0 | 8 | 0 | 0 | 9 | 7 | 0 | 7 | 67 | III |
| Л 2 Ш Г | 6 | 0 | 6 | 0 | 0 | 7 | 8 | 0 | 0 | 0 | 9 | 9 | 7 | 0 | 7 | 59 | |
| 1 5 4 3 А | 6 | 6 | 6 | 0 | 0 | 0 | 8 | 0 | 8 | 0 | 2 | 9 | 0 | 0 | 7 | 52 | |
| Летово А | 6 | 0 | 6 | 7 | 0 | 7 | 8 | 0 | 8 | 0 | 0 | 2 | 0 | 0 | 7 | 51 | |
| В Ш Э Е | 6 | 6 | 6 | 0 | 2 | 7 | 0 | 0 | 0 | 9 | 0 | 6 | 0 | 0 | 7 | 49 | |
| В Ш Э И | 6 | 6 | 6 | 0 | 0 | 7 | 6 | 0 | 0 | 1 | 0 | 0 | 7 | 2 | 7 | 48 | |
| Л 2 Ш А | 6 | 0 | 6 | 0 | 0 | 6 | 8 | 0 | 2 | 0 | 6 | 7 | 0 | 7 | 48 | ||
| Школково А | 6 | 0 | 6 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 9 | 5 | 7 | 0 | 7 | 47 | |
| 1 5 1 1 В | 6 | 6 | 6 | 0 | 0 | 0 | 8 | 0 | 0 | 1 | 0 | 0 | 5 | 7 | 39 | ||
| 3 6 6 Б СПб | 6 | 0 | 6 | 7 | 0 | 0 | 4 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 7 | 38 | |
| 1 5 8 0 Г | 6 | 0 | 6 | 0 | 0 | 0 | 8 | 0 | 8 | 1 | 1 | 0 | 7 | 0 | 0 | 37 | |
| Ф Т Л Б Долгопр. | 6 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 8 | 1 | 0 | 0 | 0 | 0 | 7 | 35 | |
| 3 6 6 А СПб | 6 | 6 | 6 | 5 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 34 | |
| 1 5 5 7 Б | 6 | 6 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 0 | 7 | 0 | 0 | 34 | |
| В Ш Э В | 6 | 6 | 5 | 2 | -1 | 7 | 8 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 34 | ||
| 2 1 8 Б | 6 | 0 | 6 | 7 | 0 | 6 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 33 | |
| 2 0 0 7 Ш | 6 | 6 | 6 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 33 | |
| В Ш Э Б | 6 | 6 | 6 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 1 | 30 | |
| Ф М Л А Дубна | 6 | 6 | 6 | 6 | 0 | 0 | 2 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 29 | |
| 1 5 1 1 А | 6 | 6 | 6 | 0 | 0 | 0 | 8 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 3 | 28 | |
| 2 3 В Подольск | 6 | 0 | 6 | 0 | 0 | 6 | 6 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 27 | |
| Ф М Л Б Дубна | 6 | 0 | 6 | 0 | -1 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 1 | 26 | |
| 1 5 5 7 А | 6 | 6 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 2 | 3 | 0 | 0 | 0 | 22 | |
| 2 1 2 0 Б | 6 | 0 | 6 | 0 | 0 | 0 | 8 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 21 | |
| 1 5 1 1 Б | 0 | 0 | 0 | 5 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 3 | 3 | 7 | 20 | |
| 2 0 0 7 З | 6 | 6 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 19 | |||
| 1 5 1 1 Г | 6 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 6 | 0 | 0 | 0 | 18 | |
| Цифр. школа Б | 6 | 6 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 | |
| 1 5 1 8 К | 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 16 | |
| 1 5 2 0 А | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 7 | 14 | |
| 1 3 0 2 В | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 13 | |
| 1 5 1 8 Ж | 6 | 0 | 6 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | |
| 1 5 5 7 В | 6 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | |
| 2 0 1 0 В | 0 | 6 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | |
| 1 2 5 3 Г | 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 1 3 0 2 А | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 7 | |
| 1 5 2 0 Б | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 7 | |
| 1 9 8 1 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 1 | 7 | ||
| 1 5 1 8 З | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 3 | |||
| Светлые горы А | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | |
| 1 5 8 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 1 5 8 В | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 8 6 7 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 1 7 3 А | 0 | ||||||||||||||||
| 1 3 0 2 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 3 7 0 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 3 7 0 Г | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 4 6 6 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 5 1 4 Б | 0 | ||||||||||||||||
| 1 5 1 8 Б | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | 0 | 0 | 0 | 0 | ||||
| М М Ш В | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 5 8 Д | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | -1 | |