XXV Турнир имени М. В. Ломоносова

1 октября 2000 года

Отчёт

МЦНМО
МОСКВА 2001

Конкурс по физике

Задания

После номера задачи в скобках указано, каким классам эта задача рекомендуется. Работы учеников 6 класса и младше оцениваются по двум, 7-8 классов - по трём, 9-11 классов - по четырём лучше всего решённым задачам. Решать больше задач и задачи класса старше своего - можно. Решённая задача класса младше своего оценивается существенно ниже.

1. (6-8) Во время грозы расстояние от себя до места, где ударила молния, можно примерно определить таким способом.

Сразу, как сверкнёт молния, начать считать секунды: "раз, два, три, четыре, ...", до тех пор, пока не прогремит гром. Последнее названное число разделить на 3 - получится примерное расстояние в километрах от места наблюдения до места удара молнии.

На чём основан этот способ и почему нужно делить именно на 3? Почему этот способ не очень точный? (Перечислите основные причины.)

2. (6-8) В Москве на некотором участке Садового кольца (длина участка 1 км) средняя скорость движения автотранспорта в правом ряду - 5 км/ч, в двух средних - 6 км/ч, в левом - 7 км/ч. В каждом ряду помещается одинаковое количество машин. Найти среднее время, за которое машины проезжают этот участок Садового кольца.

3. (7-8) Пассажир заметил, что стакан чая в вагоне-ресторане поезда во время движения остывает быстрее, чем на остановках. Предложите физическое объяснение этого явления.

4. (6-11) Ясным весенним днём в Москве пошёл мелкий дождичек. Постройте примерную (качественную) зависимость концентрации в воздухе тополиного пуха от времени с момента начала дождичка. Объясните предложенное вами решение.

5. (9-11) Тележка едет по горизонтальной поверхности земли с постоянным ускорением. На тележке установлены две стойки одинаковой высоты (отрезок, соединяющий основания стоек, параллелен направлению движения). На этих стойках висит кусок цепочки (см. рис.). По рисунку определить направление движения и приблизительно ускорение a, с которым движется тележка. Описать способ определения ускорения по рисунку и привести его обоснование. Считать g=10 м/с².

6. (8-11) Между клеммами A и B параллельно подключили две одинаковые цепочки из трёх последовательно соединённых резисторов сопротивлениями R, 2R и R. Параллельно каждому из резисторов сопротивлением 2R подключили две такие же цепочки -R-2R-R-, а сами резисторы сопротивлением 2R, параллельно которым подключали цепочки, отметили (чтобы не запутаться). Параллельно каждому из неотмеченных резисторов сопротивлением 2R опять подсоединили по две цепочки -R-2R-R-, а сами резисторы сопротивлением 2R, параллельно которым подключали цепочки, отметили. Такую операцию повторили бесконечное количество раз. Найти сопротивление R_AB между клеммами A и B.

7. (9-11) Между гладкой табуреткой и стулом такой же высоты (горизонтально) лежит доска длины L массы M (масса равномерно распределена по длине). Коэффициент трения между доской и стулом m, между доской и табуреткой - 0. На табуретке сидит мышь массы m. Увидев кошку, мышь перебегает по доске с табуретки на стул, рассчитывая свои действия так, чтобы на стуле оказаться как можно быстрее и при этом не свалить доску, опирающуюся на самый край стула. Найдите работу A, совершённую мышью во время перебегания по доске. Мощность мыши не ограничена, её лапы по доске не проскальзывают.

8. (10-11) Ясным солнечным днём Шерлок Холмс сидел у окна, разглядывая заголовок газеты в свою любимую большую стеклянную лупу. Оказалось, увеличенное изображение в середине лупы воспроизводится практически без искажений, а по краям вдоль границ чёрных букв видны цветные полосы: жёлтые со стороны края лупы и синие - со стороны её центра.

Объясните наблюдаемое явление и заполните (все или некоторые) пропуски в таблице (напишите, почему выбран именно такой цвет):

Объект наблюдения (на белой бумаге). Цвет полосы вдоль ближнего к центру лупы края изображения. Цвет полосы вдоль ближнего к краю лупы края изображения.

Чёрные печатные буквы. Синий. Жёлтый.

Линия от красного фломастера.

Линия от зелёного фломастера.

Линия от тёмно-синей шариковой ручки. Жёлтый (между жёлтой полосой и изображением - тонкая красная полоска).

(При наличии правильного исчерпывающего объяснения задача считается решённой независимо от наличия правильно заполненной таблицы, в остальных случаях таблица учитывается.)

Ответы и решения к заданиям конкурса по физике

Cразу, как сверкнёт молния, начать считать секунды "раз, два, три, четыре, ..." до тех пор, пока не прогремит гром. Последнее названное число разделить на 3 - получится примерное расстояние в километрах от места наблюдения до места удара молнии.

Решение. После удара молнии свет вспышки доходит до нас практически мгновенно (скорость света c=299792,458 км/с), а скорость звука в воздухе:
при температуре 0 ^oC - приблизительно 331 м/с = 1/3,021... км/с = приблизительно 1/3 км/с;
при температуре 20 ^oC - приблизительно 343 м/с = 1/2,915... км/с = приблизительно 1/3 км/с.

В интервале температур воздуха 0 ^oC - 20 ^oC (во время грозы температура воздуха обычно лежит в этих пределах) можно считать, что за 1 секунду звук проходит 1/3 км, за 3 секунды - 1 км. Поэтому, чтобы узнать количество километров, количество секунд нужно делить на 3.

Причины ошибок:
1) неточное измерение промежутка времени ("раз, два, три, ...");
2) использованное приближённое значение скорости звука;
3) скорость звука в воздухе зависит от температуры, влажности, присутствия капель воды и др. причин, которые могут меняться (особенно во время грозы);
4) в месте прохождения канала молнии возникают ударные волны, которые распространяются по воздуху быстрее звуковых и на некотором расстоянии (пока не затухнут и не превратятся в звуковые) именно они определяют время, через которое прогремит гром;
5) звук возникает не только в месте попадания молнии в землю, но и по всей длине канала прохождения электрического разряда, которая может составлять несколько километров - сначала мы можем услышать звук, пришедший от какой-нибудь промежуточной точки, а не от места попадания в землю;
6) звук от места попадания молнии в землю мы можем вообще не услышать (например, если молния попала в лес или за возвышением), а услышим только гром, дошедший до нас от какой-то другой точки молнии, возможно, ещё и не по прямой, а в результате нескольких отражений.

Если провести более точную оценку, окажется, что причины 1 и 2 не являются главными, т. е. увеличение точности отсчёта времени и использование в расчётах более точного (чем 1/3 км/с) значения скорости звука в воздухе не увеличивают точность окончательного результата. А вот для того, чтобы узнать, приближается к нам гроза или, наоборот, удаляется - описанный способ вполне годится.

Решение. Среднее арифметическое времён проезда этого участка в каждом из рядов t_ср=(1/4)((1/5)+2(1/6)+(1/7)) ч - неправильный ответ. Дело в том, что чем больше скорость движения в ряду, тем бо'льшее количество машин по нему за определённое время. Заметим (это легко проверить), что по одному ряду проезжает машин во столько раз больше, чем по другому, во сколько раз скорость движения по нему больше, чем по другому. Поэтому при вычислении среднего арифметического слагаемые в числителе и знаменателе нужно умножить на коэффициенты, так, чтобы соответствующее этим слагаемым количество машин учитывалось правильно:

t_ср=(1/(1+(6/5)*2+(7/5)))((1/5)+(6/5)*2(1/6)+(7/5)(1/7)) ч =
=(1/(24/5))((1/5)+(2/5)+(1/5)) ч = (5/24)(4/5) ч = 1/6 ч = 10 мин.

Решение. В результате вибрации поезда во время движения поверхность чая в стакане становится неровной, увеличивается её площадь, что приводит к увеличению интенсивности испарения, на которое затрачивается тепловая энергия жидкости (при прочих равных условия (температура, влажность воздуха) количество жидкости, испаряющейся в единицу времени, пропорционально площади поверхности).

Также не следует забывать, что во время тряски стенки стакана всё время смачиваются и чай с них тоже испаряется, площадь поверхности мокрых стенок сравнима с площадью поверхности чая.

Тряска также влияет на конвекционные потоки внутри остывающего чая и на потоки воздуха над его поверхностью (движущиеся "волны" на поверхности "гоняют" воздух). Этот эффект может привести как к увеличению интенсивности охлаждения (за счёт увеличения интенсивности испарения (с поверхности) и охлаждения через стенки из-за более сильного перемешивания жидкости), так и наоборот - в результате вибрации могут разрушится конвекционные потоки.

Решение. Основные причины, по которым пушинка может перестать летать в воздухе:
1) прямое попадание в пушинку капли дождя или брызг, образовавшихся после удара капли о землю;
2) увеличение массы и плотности пушинки из-за возрастающей со временем (после начала дождя) влажности воздуха, из-за чего пушинка может "приземлиться";
3) движение пушинок вниз в потоке воздуха, увлекаемом каплями дождя, после чего пушинка может прилипнуть к мокрой земле, асфальту или поверхности лужи, или может быть сбита брызгами у поверхности земли;
4) пушинки должны иметь электрический заряд (как всякие мелкие частицы, летающие в воздухе - например пыль, прилипающая по этой причине к экрану телевизора или компьютера). На первый взгляд кажется, что, раз все тополиные пушинки примерно одинаковы и находятся в одинаковых условиях, они должны иметь примерно одинаковый электрический заряд и поэтому отталкиваться друг от друга, что помогает им "висеть" в воздухе.

На самом деле скорее всего всё устроено "хитрее". Например, тоже вроде бы одинаковые капли дождя [¹¹ Здесь приводятся данные для сильного (грозового) ливня.] заряжены по-разному - встречаются как отрицательно (их средний заряд -1,3*10^-12 Кл), так и положительно (средний заряд +1,1*10^-12 Кл) заряженные капли, причём положительно заряженных капель в среднем в 1,5 раза больше, чем отрицательно заряженных. Средний электростатический потенциал таких капель - 40 В, максимальный - около 300 В (напряжение в бытовой электросети, напомним, всего 220 В). Заряд капель "мелкого дождичка" меньше - в среднем 10^-15 Кл - 10^-14 Кл, максимум - 5*10^-13 Кл.

Распределение зарядов пушинок скорее всего также достаточно сложное. Данных о распределении зарядов в тополином пухе и даже о примерной величине зарядов пушинок нам найти не удалось (видимо, ни физики, ни биофизики, ни биологи всерьёз не интересовались этим вопросом).

Можно предположить, что пушинки похожи на снежинки (средний заряд 10^-12 Кл - 10^-11 Кл, максимальный 5*10^-11 Кл). Если такие предположения верны, то основным эффектом наличия дождика будет просто уменьшение электрического сопротивления атмосферы, что, возможно, приведёт к стеканию зарядов и уменьшению устойчивости пуха (концентрации пушинок-снежинок и дождинок примерно одинаковые, а заряд пушинки-снежинки примерно на 3 порядка (в 1000 раз) больше, чем дождинки, поэтому электростатическое взаимодействие пушинок с дождинками можно не учитывать).

Во время дождя можно заметить интересный парадокс: асфальт уже полностью мокрый (т. е. капли дождя уже перекрыли всю площадь воздуха), а пух всё ещё летает (хотя теоретически все пушинки уже должны быть "сбиты" каплями). Пух летает даже через промежуток времени, в 2-3 раза больший того, когда после начала дождя асфальт полностью намок (поправка на то, что диаметр "кляксы" от капли на асфальте больше диаметра капли в полёте). Дело тут в том, что движение капли дождя в воздухе (к моменту, когда она окажется около земли на высоте, на которой летает тополиный пух) является установившимся, воздушные потоки обтекают каплю, убирая с её пути пушинки. А вот движение брызг у земли установиться не успевает и они "сбивают" пушинки намного эффективнее.

5. (9-11) Тележка едет по горизонтальной поверхности земли с постоянным ускорением. На тележке установлены две стойки одинаковой высоты (отрезок, соединяющий основания стоек, параллелен направлению движения). На этих стойках висит кусок цепочки (см. рис. на стр. 78). По рисунку определить направление движения и, приблизительно, ускорение a, с которым движется тележка. Описать способ определения ускорения по рисунку и привести его обоснование. Считать g=10 м/с².

Решение. Тележка едет слева направо (потомучто цепочка " провисает в обратную сторону"). Заметим, что на самом деле правильнее говорить о том, что слева направо направлено ускорение (а скорость может быть направлена в противоположную сторону - в этом случае тележка движется равнозамедленно).

Определить числовое значение ускорения a можно с помощью такого алгоритма:
1) положить на рисунок линейку (или ровный край листа бумаги) так, чтобы она проходила через концы цепочки (точки прикрепления цепочки к стойкам);
2) поворачивать линейку вокруг левого конца цепочки по направлению часовой стрелки до тех пор, пока незакрытая линейкой часть изображения цепочки и сама линейка не будут ограничивать фигуру, имеющую ось симметрии (перпендикулярную линейке);
3) построить эту ось симметрии (серединный перпендикуляр к отрезку, соединяющему точки пересечения цепочки с линейкой);
4) отметить на этой оси произвольный отрезок, построить на нём как на гипотенузе прямоугольный треугольник, один катет которого вертикален, а другой - горизонтален;
5) найти a из пропорции

(длина вертикального катета)/(длина горизонтального катета)=g/a.

Обоснование. [Вектора здесь обозначены не стрелочкой сверху, а жирным шрифтом] Известно, что движение системы в поле силы тяжести g с ускорением a эквивалентно [¹² В предположении, что скорость системы нерелятивистская, то есть много меньше скорости света c] для самой системы нахождению её (равномерному прямолинейному движению c любой скоростью [¹³ много меньшей скорости света c], в частности, покою) в поле силы тяжести g-a. Направление g известно (вертикальное) - значит (в выбранном масштабе) |g| = длина вертикальной проекции отрезка = длина вертикального катета.

Мысленно закрепим цепочку в точке, в которой на рисунке она пересекается с линейкой. Очевидно, форма цепочки от этого не изменится (система находилась в равновесии до этого и будет находиться после). Теперь у нас есть подвешенный за концы кусок цепочки, имеющий симметричную форму. Именно так должен висеть кусок цепочки в поле тяжести, параллельном оси симметрии.

Тем самым ось симметрии - это направление векторной разности g-a. Выберем на этом направлении отрезок и будем считать, что мы выбрали масштаб таким образом, что его длина равна |g-a|.

Направление a горизонтально по условию - "Тележка едет по горизонтальной поверхности земли с постоянным ускорением.", поэтому

|a| = длина горизонтального катета. Поэтому отношение длин векторов |g|/|a| равно отношению длин катетов, то есть верна пропорция

(длина вертикального катета)/(длина горизонтального катета)=g/a,

что и требовалось обосновать.

Справка (эти сведения не являются необходимыми для решения задачи). Кривая, форму которой имеет висящая в поле силы тяжести однородная цепочка, является графиком функции "гиперболический косинус" (Здесь важно, что цепочка гнётся в любом месте без какого-либо сопротивления, для верёвки это будет не так и поэтому форма подвешенного за концы куска верёвки будет другой). Другое название графика функции "гиперболический косинус" - цепная линия (т. е. линия висящей цепи): (e^x+e^-x); e=2,718281828459045...

Предполагается, что координатная ось x направлена горизонтально, ось y - вертикально. Если концы цепочки закреплены в точках с координатами (X; ch(X)) и (-X; ch(X)), она имеет длину

L=e^X+e^-X

Конечно, между точками (X; ch(X)) и (-X; ch(X)) можно подвесить цепочку какой-нибудь другой длины. Тогда форма цепочки не будет совпадать с графиком функции ch(x). Часто говорят, что форму гиперболической косинусоиды имеют все цепочки, висящие в однородном поле тяжести.

Оказывается, что все гиперболические косинусоиды (геометрически) подобны друг другу: если у нас есть фотографии двух висящих цепочек, мы всегда можем увеличить одну из фотографий так, чтобы при наложении её на другую фотографию изображения цепочек совпали (разумеется, могут быть "хвосты", которые не накрываются изображением цепочки с другой фотографии, но накладывающиеся участки совпадают точно).

Зная факты, описанные после слова "справка" и до этой строчки, можно (хотя и не очень просто) "школьными" методами получить уравнение для формы цепочки любой данной длины, висящей между двумя любыми данными точками. Предлагаем Вам над этим подумать.

Замечание. Наличие оси симметрии в п. 2 определяется на глаз. После этого правильность положения линейки лучше проверить и при необходимости уточнить (например, проверить, что расстояние от точки пересечения цепочки с построенной осью симметрии до концов прямолинейного участка границы фигуры одинаковы). Если это не так - чуть подвинуть линейку. Двух уточнений обычно бывает достаточно.

Решение. Пусть x>0 - сопротивление такой схемы:

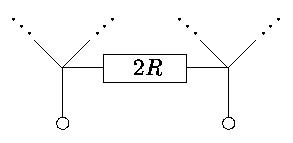
Последовательно преобразуем схему следующим образом:

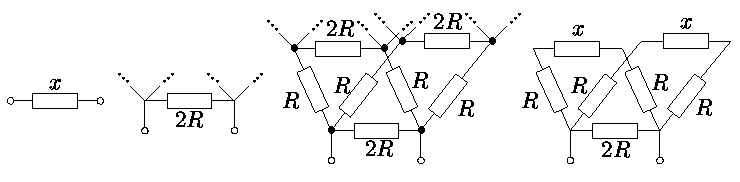
1/x=(1/(2R))+(1/(R+x+R))+(1/(R+x+R))

1/x=(1/(2R))+(2/(2R+x))=(2R+x+2*2R)/(2R(2R+x))=(6R+x)/(4R²+2Rx)

x=(4R²+2Rx)/(6R+x)

6Rx+x²=4R²+2Rx

x²+4Rx-4R²=0

x=(-4R+((4R)²-4(-4R²))^1/2)/2= R>=(-4R+(32R²)^1/2)/2=(-4R+4R*2^1/2)/2=2R(+2^1/2-1)

x>0, следовательно x=2R(2^1/2-1)

Сопротивление x получилось в результате параллельного соединения R_AB и 2R.

1/x=(1/R_AB)+(1/(2R))

1/(2R(2^1/2-1))=(1/R_AB)+(1/(2R))

1/R_AB=(1/(2R(2^1/2-1)))-(1/(2R))=(1/(2R))((1/(2^1/2-1))-1)=(1/(2R))((2-2^1/2)/(2^1/2-1))

R_AB=2R(2^1/2-1)/(2-2^1/2)=2R((2^1/2-1)(2+2^1/2))/((2-2^1/2)(2+2^1/2))=2R(2^1/2/2)=2^1/2R

Ответ. R_AB=2^1/2R.

Решение. Мышь в каждой точке доски может двигаться с ускорением не больше некоторого (зависящего от точки), а её скорость при этом, очевидно, может быть любой. Ускорение определяется из условия, что горизонтальная сила, с которой мышь действует на доску (F=ma), не должна быть больше максимальной силы трения покоя доски о стул. Эта сила трения F_тр=mN, где N - сила реакции стула, действующая на конец доски, который на этом стуле лежит.

Пусть мышь находится на доске на расстоянии x от табуретки. Чтобы доска была неподвижной (как требуется в условии задачи) необходимо, чтобы сумма моментов сил, действующих на доску, относительно конца доски, лежащего на табуретке, была равна 0.

Mg(L/2)+mg(L-x)-NL=0

(силу трения мыши о доску не учитываем, т. к. конец доски лежит на прямой, вдоль которой действует эта сила, поэтому момент этой силы относительно этого конца равен 0)

NL=Mg(L/2)+mg(L-x)

N(x)=(Mg(L/2)+mg(L-x))/L=(-mg/L)x+((Mg/2)+mg)

Видим, что зависимость силы реакции N (и, следовательно, максимальной силы трения покоя F_тр=mN) от положения мыши на доске - линейная.

Следовательно, мышь в каждый момент времени должна двигаться с максимально возможным ускорением. Поскольку это ускорение везде положительно (мышь нигде не тормозила), а доска горизонтальна, совершённая мышью работа равна кинетической энергии (когда мышь находилась в конце доски, в начале скорость мыши по условию была равна 0).

Построим график зависимости ускорения от координаты. Поскольку эта зависимость линейная, площадь под графиком S легко найти школьными методами. Из известной формулы 2ax=v²-v₀² (или ax=(v²/2)-(v₀²/2) следует, что эта площадь равна изменению половины квадрата скорости за время движения, то есть (так как у нас v₀=0) это просто v²/2.

Работа мыши, которую нужно найти, A=mv²/2=mS.

F_max(0)=m(M/2)g; F_max(L)=m((M/2)+m)g.

a_max(0)=(1/m)F_max(0)=(1/m)m(M/2)g; a_max(L)=(1/m)F_max(L)=(1/m)m((M/2)+m)g.

S=L(a_max(0)+a_max(L))/2=(L/(2m))mg((M/2)+(M/2)+m)=Lmg((M+m)/(2m)).

Ответ: A=mS=mLmg((M+m)/(2m))=(1/2)m(M+m)gL.

Примечание. На первый взгляд может показаться, что при решении этой задачи проще воспользоваться формулой

работа = сила * перемещение

Однако для обоснования минимальности времени нам всё равно придётся искать ускорение, а когда мы его уже нашли - довести решение до конца оказывается проще приведённым выше способом.

8. (10-11) Ясным солнечным днём Шерлок Холмс сидел у окна, разглядывая заголовок газеты в свою любимую большую стеклянную лупу. Оказалось, увеличенное изображение в середине лупы воспроизводится практически без искажений, а по краям вдоль границ чёрных букв видны цветные полосы - жёлтые со стороны края лупы и синие - со стороны её центра.

Объясните наблюдаемое явление и заполните (все или некоторые) пропуски в таблице (напишите, почему выбран именно такой цвет).

См. таблицу в условии на стр. 79.

Решение. В солнечном свете (и, разумеется, его отражении от белой бумаги) содержится весь спектр цветов (радуга). Стекло обладает дисперсией, то есть преломляет лучи разных длин волн (цветов) под разными углами.

Чистую белую бумагу сквозь лупу мы также видим белой, т. е. от каждой точки поверхности лупы к нам в глаз направляются все спектральные компоненты. Но отражены они от разных участков поверхности бумаги (расположенных друг за другом в порядке цветов спектра (этот порядок, соответствующий, последовательности цветов полос радуги, легко запомнить с помощью известной фразы про фазана и охотника).

Когда, из-за наличия на участках поверхности бумаги рисунка, от этих участков отражаются не все спектральные компоненты, в некоторых местах спектр оказывается неполным, что и воспринимается нами как цветные полосы.

Обычное стекло [¹⁴бывают стёкла и кристаллы, которые ведут себя наоборот, но лупы из них обычно не делают.] сильнее преломляют спектральные компоненты с меньшей длиной волны (в "синей" области спектра).

Чтобы объяснить, что именно происходит при рассматривании в лупу полос разного цвета, для простоты будем считать, что белый свет состоит всего из трёх компонент: синей (направление лучей которой меняется лупой сильнее всего), жёлтой и красной (направление лучей меняется слабее всего). Белая бумага отражает все компоненты, цветные полосы на ней отражают только "свой" цвет, а чёрные не отражают вообще ничего.

Каждый Охотник Желает Знать Где Cидит Фазан

Красный Оранжевый Жёлтый Зелёный Голубой Cиний Фиолетовый

l, нм 600-760 570-590 510-560 480-500 380-470

Детская считалка для запоминания последовательности цветов спектра (радуга)

Рассмотрим какую-нибудь точку (A) на белой бумаге и точку A' на изображении бумаги в лупе, в которую из точки A попадают лучи жёлтого цвета, а также точку O на бумаге, изображение которой O' находится в центре изображения участка бумаги, даваемого лупой. Тогда лучи жёлтого цвета в точку A' попадают из некоторой точки B, а лучи синего цвета - из точки C. Точки A, O, B, C находятся на бумаге на одной прямой в порядке O-C(синий)-A(жёлтый)-B(красный). (Синие лучи преломляются лупой на самый большой угол, красные - на самый маленький).

Проведём теперь по бумаге чёрную полосу около точки A ближе к точке O (точка C оказалась на этой полосе, а точка A - на ближайшем к кра'ю лупы краю' этой полосы). Теперь точка изображения A' будет казаться жёлтой (лучи красного и жёлтого цвета из точек B и A в точку A попадаю, а лучи синего цвета из точки C - нет, так как теперь она покрашена в чёрный цвет и вообще никаких лучей не отражает; смесь жёлтого и красного цвета видна как жёлто-оранжевый). Этим и объясняется жёлтая окраска этого края полосы.

Аналогично, если провести чёрную полосу с другой стороны точки A (по точке B) - мы увидим точку A' в синем цвете (так как от чёрной точки B в точку A' теперь не попадают красные лучи).

Так же объясняется и окраска краёв изображений цветных полос.

Описанное выше явление искажения цвета при формировании изображения в линзах (и других оптических системах) носит название хроматическая аберрация.

Правильно заполненная таблица (данные условия задачи напечатаны обычным шрифтом, пустые клетки заполнены курсивом; надеемся, что у Шерлока Холмса была такая же лупа, как и у жюри, даже если и не так - различия будут не очень значительными).

Объект наблюдения (на белой бумаге). Цвет полосы вдоль ближнего к центру лупы края изображения. Цвет полосы вдоль ближнего к краю лупы края изображения.

Чёрные печатные буквы. Синий. Жёлтый.

Линия от красного фломастера. Синий (фиолетовый). Жёлтый.

Линия от зелёного фломастера. Полоса не наблюдается. Жёлтый.

Линия от тёмно-синей шариковой ручки. Синий (голубой). Жёлтый (между жёлтой полосой и изображением видна тонкая красная полоска).

Объект наблюдения (на белой бумаге).	Цвет полосы вдоль ближнего к центру лупы края изображения.	Цвет полосы вдоль ближнего к краю лупы края изображения.
Чёрные печатные буквы.	Синий.	Жёлтый.
Линия от красного фломастера.
Линия от зелёного фломастера.
Линия от тёмно-синей шариковой ручки.		Жёлтый (между жёлтой полосой и изображением - тонкая красная полоска).

	Каждый	Охотник	Желает	Знать	Где	Cидит	Фазан
	Красный	Оранжевый	Жёлтый	Зелёный	Голубой	Cиний	Фиолетовый
l, нм	600-760	570-590		510-560	480-500	380-470