Задания
В скобках указано, каким классам адресована задача. Ваше выступление по математике считается успешным, если правильно решены хотя бы две задачи, адресованные Вашему или более старшему классу. Верное решение только одной задачи также будет отмечено жюри.
1. (7-9) На протяжении некоторого года (от 1 января до 31 декабря включительно)
количество вторников было равно количеству четвергов. Следует ли из этого,
что и количество сред было такое же? Рассмотрите два случая:
а) в году было 365 дней,
б) в году было 366 дней.
2. (7-9) Все натуральные числа от 1 до 1000 включительно разбиты на две группы: чётные и нечётные. В какой из групп сумма всех цифр, используемых для записи чисел, больше и на сколько?
3. (8-9) Известно, что х=2а5=5b2>0, числа а и b - целые. Каково наименьшее возможное значение х ?
4. (7-10) Даны прямая и точка вне неё.
Как с помощью циркуля и линейки построить прямую, параллельную данной
прямой и проходящую через данную точку, проведя при этом возможно меньшее
число линий (окружностей и прямых), так что последняя проведённая линия -
это искомая прямая? Какого числа линий Вам удалось добиться?
5. (8-11) Дан квадрат со стороной 1.
Каждая его сторона разбита на три равные части.
Через точки деления проведены отрезки (см. рисунок).
Найдите площадь заштрихованного квадратика.

6. (8-11) Разделим каждое четырёхзначное число на сумму его цифр. Какой самый большой результат может получиться?
7. (10-11) Многогранник вписан в сферу. Может ли оказаться, что этот многогранник невыпуклый? (Многогранник вписан в сферу, если все концы его рёбер лежат на сфере.)
Решения к заданиям конкурса по математике
1а. В году 365 дней, то есть 52 полные недели плюс один день. Если год начинается со среды (например, 2003-ий год), то сред будет на одну больше, чем вторников и четвергов.
Ответ: не следует.
1б. 366 дней - это 52 недели и ещё 2 дня. Они не могут быть вторником и четвергом, так как эти дни идут не подряд. Не один из этих дней не среда, потому что иначе другой день был бы вторником или четвергом, и при этом нарушается условие равенства вторников и четвергов. Значит, сред в году не больше и не меньше.
Ответ: следует.
2. Сумма цифр числа 1 равна сумме цифр числа 1000; остальные числа разобьём на пары: 2-3, 4-5, 6-7, 8-9,..., 998-999. В каждой паре единицы нечётного числа больше на 1, чем чётного, а десятков и сотен у них поровну. Всего таких пар 499.
Ответ: сумма цифр нечётных чисел больше на 499.
3. Число х делится на 2 и на 5. х=2а5, поэтому а делится на 5. Так как x=5b2, то х делится на 22, значит а делится и на 2 тоже. Предполагая а=2*5=10, получим х=200000 и b=200.
Ответ: 200000.
4. Дана прямая a и точка O (обозначения). Отметим
на прямой две произвольные точки A и B. Проведём окружность
с центром в точке B радиуса AO, и окружность с центром в
точке O радиуса AB. Они пересекутся в точке X.
Четырёхугольник AOXB - параллелограмм, так как его противолежащие
стороны равны. Теперь можно провести искомую прямую - OX.
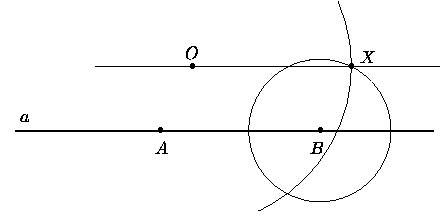
Излагая это же решение другими словами, можно сказать, что мы стандартным способом построили треугольник BOX по двум вершинам (B и О) и длинам двух сторон, равных длинам отрезков AO и AB. Очевидно, что DABO=DXOB (по трём сторонам). Поэтому угол ABO = угол XOB, а это внутренние накрестлежащие углы для прямых a и OX и секущей BO. Из равенства этих углов следует, что a и OX параллельны.
Другое решение. Отметим на прямой произвольную точку A
и проведём через точку O окружность с центром в точке A.
Эта окружность пересекает прямую в двух точках; обозначим их через М
и N.
Далее измерим [1 см. разъяснение на
стр. 11]
циркулем отрезок MO и проведём с центром в точке N окружность
радиуса MO. Искомая прямая проходит через точку O
и точку B пересечения двух построенных окружностей.
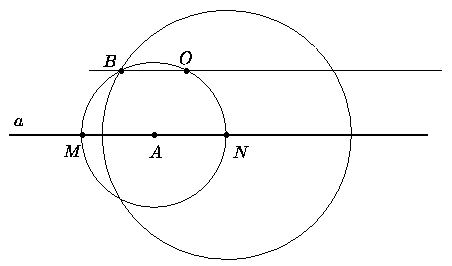
DMAO=DNAB по трём сторонам, следовательно, равны и высоты этих треугольников, проведённые из вершин O и B. Основания этих треугольников (MA и NA) лежат на прямой a, поэтому точки O и B находятся от прямой a на одинаковом расстоянии.
Недостатком этого решения является то, что если точка A случайно оказалась основанием перпендикуляра, проведённого из точки O, то точки O и B совпадают и не определяют нужной нам прямой.
Тем не менее, ученикам, приводившим такое решение, оно засчитывалось полностью (ставилась оценка +) [2 На самом деле этот же недостаток "замаскирован" и в первом решении, в предложении "Отметим на прямой две произвольные точки A и B." Если точки произвольные, то они случайно могут совпасть (и тогда построение не получится), а для построения на прямой двух несовпадающих точек придётся проводить дополнительные линии.].
Докажем теперь, что двумя линиями обойтись нельзя. Второй линией должна стать искомая прямая. Чтобы её провести, нужно получить вторую точку, находящуюся на том же расстоянии от прямой a, что и точка O. Но после проведения одной линии все точки этой линии, кроме точек пересечения с прямой a, будут неразличимы, и найти вторую точку, находящуюся на нужном расстоянии от прямой a, построив только одну линию, невозможно.
Ответ: 3 линии.
Пояснение. В решении мы упоминали параллелограмм, треугольники, секущую BO и углы. Однако для построения нам были нужны только точки (вершины параллелограмма и треугольников, концы отрезка секущей, концы отрезков, образующих углы), сами же отрезки для построения нужны не были, поэтому мы их не проводили и, разумеется, не учитывали при подсчёте проведённых линий.
5. Обозначим длину стороны заштрихованного квадратика (рисунок на стр. 7) через х. Заметим, что все наклонные отрезки имеют длины х, 2х/3 и х/3, это следует из теоремы Фалеса. Тогда, сложив вместе трапецию со сторонами х, х, 2х/3, 1/3 и треугольник со сторонами х, 1/3, х/3, мы получим квадратик, равный заштрихованному. Аналогично можно сложить квадратик из двух трапеций со сторонами х, х/3, 1/3, 2х/3. Всего получится 10 одинаковых квадратиков суммарной площади 1. Значит, площадь каждого квадратика равна 1/10.
Можно решить задачу, используя теорему Пифагора, запишем её для самого маленького на рисунке треугольника:
x2 + (x/3)2 = (1/3)2
Решение уравнения x=1/(101/2).
Ответ: площадь равна 1/10.
6. Ответ: 1000/1=1000.
Докажем, что больше 1000 получить невозможно. Пусть число записано цифрами a b c d. Если a b c d > a 0 0 0 , то a b c d < (a+1) 0 0 0, а сумма его цифр S>a+1, поэтому частное будет меньше 1000.
Другое рассуждение.
(1000a+100b+10c+d)/(a+b+c+d) =
= ((999a+99b+9c)/(a+b+c+d))+1 > ((999a+99b+9c)/(a+b+c))+1 =
= ((990a+90b)/(a+b+c))+10 > ((990a+90b)/(a+b))+10 =
= ((900a+90b)/(a+b))+100 > (900a/a)+100 = 1000
7. Приведём пример невыпуклого многогранника, вписанного в сферу. Возьмём правильный октаэдр, опишем вокруг него сферу. Теперь возьмём две его соседние грани ABC и BCD, удалим их вместе с ребром BC, а вместо этого добавим ребро AD и грани ABD и ACD. Отрезок BC больше не принадлежит фигуре, поэтому она невыпуклая. Но вершины у этого многогранника, те же, что и у правильного октаэдра. Следовательно, многогранник вписанный [3 Художественное изображение получившегося таким образом невыпуклого вписанного многогранника см. на обложке.]
Можно было действовать следующим образом. Возьмём куб и проделаем в нём "дырку" в виде прямоугольного параллелепипеда (сквозь две параллельные грани куба). Затем восемь точек, краёв "дырки", соединим рёбрами с ближайшими вершинами куба и "поднимем" ("опустим") их на сферу, описанную вокруг куба.