XXV Турнир имени М. В. Ломоносова

29 сентября 2002 года

Задания. Решения. Комментарии

МЦНМО
МОСКВА 2003

Конкурс по математическим играм

Когда-то конкурс по математическим играм был традиционным на Ломоносовском турнире. В этом году, после некоторого перерыва, конкурс в порядке эксперимента был организован снова и проводился только в МГУ для участников не старше 8 класса. Как и во всяком эксперименте, не всё получилось сразу - например, условия потом пришлось немного отредактировать [⁴ Не удивляйтесь, если обнаружите небольшие различия между условиями, выданными вам на турнире, и текстами, опубликованными в этой книжке.].

Многие игры (описания, решения, программные реализации) ломоносовских турниров опубликованы в интернете по адресу http://mathgames.mccme.ru

Условия игр

1. Двое по очереди красят в свой цвет узлы бесконечной клетчатой бумаги. Побеждает тот, кто первым поставит четыре свои точки в вершинах квадрата.

2. Нарисовано по кругу 12 кружочков. Игроки по очереди ставят в кружки числа от 1 до 12. Ходить можно куда угодно, но повторять числа нельзя и требуется соблюдать правило: рядом стоящие числа должны отличаться на 1. Кто не может сделать ход - проиграл.

3. Игроки ломают "клетчатую" шоколадку m*n, меньшую часть съедают (если равны - любую), а оставшуюся дают сопернику. Кто не может ломать - проиграл. Кто выигрывает при правильной игре, если
а) m=2 , n=6
б) m=5 , n=7
в) m=10 , n=15
г) m=4 , n=9

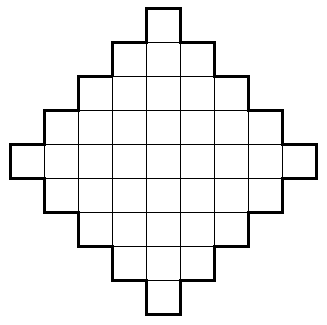
4. Рассмотрим доску, изображённую на рисунке.

Её внешняя граница нарисована толстыми линиями, а внутренние отрезочки - тонкими. Двое ходят по очереди. Каждый ход - превращение одного тонкого единичного отрезочка в толстый. Если при ходе одного игрока вся граница некоторой клетки стала толстой, то в этой клетке он ставит крестик, если это первый игрок, и нолик (нолики), если это второй игрок. (Если толстый отрезок возник между двумя соседними клетками, уже обведёнными толстой "рамочкой", то после такого хода каждая из этих двух клеток будет ограничена толстыми отрезками. В этом случае игрок, делающих ход, ставит по одному своему знаку - крестику или нолику - в обе клетки). В конце игры все клетки доски будут помечены крестикам и ноликами. Побеждает тот, чьих знаков окажется больше.

5. Двое играют на доске 8*8, закрашивая её клетки - каждый в свой цвет (красный и синий для первого и второго игрока соответственно). В начальный момент времени клетка a1 закрашена в красный цвет, h8 в синий. За ход игрок красит одну из незакрашенных клеток, соседних (по вертикали или горизонтали) с последней закрашенной его цветом, в свой цвет - "ведёт змейку". Красить повторно или перекрашивать закрашенные противником нельзя! Кто не может сделать ход - проиграл.

6. Два игрока по очереди закрашивают (в один и тот же цвет) клетки в прямоугольнике m*n, m<n, так, чтобы ни одна строка и ни один столбец не оказались бы полностью закрашенными. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре, если:
а) m=2
б) m=3
в) m=4 , n=6
г^*) m=4 , n=5.

Описания выигрышных стратегий и комментарии

Конкурс "Математические игры" большинству участников понравился, ребята с интересом играли и между собой и с ведущими. Однако, несмотря на пояснения и примеры, приводимые ведущими в начале каждого сеанса игр, многие так и не поняли, что такое стратегия игрока и как её описать. Некоторые просто писали: "первый игрок победит" или "второй победит", не указывая, как именно ему следует играть, другие ограничивались общими указаниями типа "первый должен играть так, чтобы второму стало некуда ходить".

Игрока, против которого мы играем, в играх принято называть "соперником" или "противником", но в работах некоторых школьников "противник" быстро превращается в "недруга" и даже во "врага": "Нужно подставить своего недруга", "Нужно не оставить врагу никаких шансов", и уж совсем агрессивно: "Ни в коем случае нельзя ставить много квадратов на своей территории, а как можно прогрессивней двигаться на врага!"

Игра N 1 (построение квадрата).

Эта довольно известная игра вызвала большой интерес у участников конкурса. Большинство ребят обнаружило, что первый игрок форсированно выигрывает, вынуждая противника ходить определённым образом и вскоре ставит "вилку". Стороны квадратов вовсе не обязательно расположены по линиям сетки; как написал один из участников, семиклассник Миша Гусев, "ставя отвлекающие точки, преследовать основную цель: большой, размашистый квадрат со сторонами не по линиям клеточек". Несмотря на то, что общий стиль игры ясен, точно описать стратегию непросто.

Ходы первого игрока будем обозначать крестиками, а ходы второго - кружочками. Первый игрок ставит на плоскости произвольную точку A. Пусть соперник отвечает ходом в точку X. Тогда первый ходит в точку B центрально симметричную точке A относительно точки X.

Очевидно, отрезок AB является диагональю единственного квадрата ACBD. Далее возможны две ситуации:
1) второй игрок ходит в точку C или точку D;
2) второй игрок ходит в любую другую точку Y.

Ситуация 1. Будем считать, что второй поставил точку D. Отрезок AB является стороной ровно двух квадратов. ABEF и ABE'F' (будем считать, что точка C - это центр первого квадрата, а точка D - центр второго). Тогда первый отметит точку E. Второй вынужден ходить в точку F. Теперь первый ходит в точку E'. Очевидно, второй не может дополнить точки D, F и X до квадрата, поэтому он проигрывает при следующем ходе первого (первый может дополнить любой из треугольников EAE' или ABE' до квадрата, а второй может помешать только одному из этих ходов).

Ситуация 2. Без ограничения общности можно считать, что квадрат ABE'F' и точка Y находятся в разных полуплоскостях относительно прямой AB. Пусть отрезок CX является диагональю квадрата CZXT. Если точка Y совпадает с одной из точек Z или T, то первый ходит в точку C, иначе (этот случай показан на рисунке) ему следует отметить точку D.

В последнем случае второй вынужден ходить в точку C. Первый ходит в точку E'. Заметим, что так как точка Y не совпадает ни с одной из точек Z или С, второй не может дополнить свои точки X, Y и C до квадрата. Возникшая ситуация называется "вилкой": если второй сделает ход в точку F', то первый следующим ходом дополнит треугольник BDE' до квадрата (точка Y этому не помешает, так как она лежит в другой полуплоскости относительно прямой AB) и выиграет; если же второй сделает ход в точку H, то первый построит квадрат ABE'F' (точка Y не помешает по той же причине) и всё равно выиграет.

Оставшийся случай разбирается аналогично.

Игра N 2 (числа в кружочках).

Эта игра оказалась трудной для участников конкурса. Второй игрок может победить в ней, придерживаясь довольно общего для многих игр принципа симметрии. В данном случае на ход первого игрока второй должен ставить в противоположный кружочек игрового поля число, дополняющее число первого до 13. Такой ход, очевидно, всегда возможен и не нарушит правил: если число y поставлено первым игроком рядом с x и |x-y|=1, то рядом окажутся 13-x и 13-y, но |13-x-(13-y)|=|x-y|=1. Таким образом ходы у первого игрока вскоре кончатся, и он проиграет.

Играя подобным образом, второй игрок победит при любом чётном числе кружков. При нечётном числе кружков авторы не знают стратегии ни для первого, ни для второго игрока.

Игра N 3 (разламывание шоколадки).

Игра эта может быть исследована так называемым "методом выигрышных и проигрышных позиций". Позицией в игре являются размеры очередного куска шоколадки (того, который будут ломать следующим ходом).

Назовём позицию проигрышной, если любой ход того, кому сейчас ходить, приводит к поражению (при разумной игре соперника). Напротив, позиция выигрышная, если тот, кому сейчас ходить, может сделать такой ход, что в результате победит, как бы ни играл соперник. Очевидно, что позиция, из которой можно сделать ход в проигрышную, выигрышная, а позиция, все ходы из которой проводят к выигрышной позиции, - проигрышная. В нашей игре позиции удобно изображать клетками бесконечной угловой таблицы, где по горизонтали отмечается длина, а по вертикали ширина шоколадки. В выигрышных клетках поставим "+", а в проигрышных "-". В клетке (1; 1), конечно, "-". Во всех клетках, откуда в неё можно попасть (а это (1; 2) и (2; 1) ), ставим "+". Там, откуда все ходы приводят к плюсам, ставим "-", и таблица постепенно заполняется. Правила перемещения по таблице, очевидно, такие: "можно ходить или влево, или вниз, причём ширина (в первом случае) и длина шоколадки (во втором случае) может уменьшиться не более чем в 2 раза".

В качестве примера приводим несколько последовательных шагов заполнения таблицы, начиная с левого нижнего угла. Каждый раз мы проверяем, нет ли клеток, откуда по правилам можно попасть только на "+" (если такие клетки находятся - ставим там "-"). А слева и сверху от каждого "-" рисуем "хвосты" из знаков "+", заполняя все клетки, из которых можно попасть в рассматриваемую клетку со знаком "-". Длина "хвоста" в горизонтальном (вертикальном) направлении, очевидно, равна номеру столбца (строки) данной клетки, считая слева (снизу). Первые 5 таблиц получены последовательно друг за другом, в конце мы приводим в качестве примера угол размером 14*15 (в него "помещается" условие пункта в).

              -
      +       + -
-     - +     - + -

                 -
+                +
+                + -
+ +              + +
- +              - + -
+ - + +          + - + + -
- + - + + +      - + - + + + -

                                . . . . . . . . . . . . . . . .
+                               + + + + + + + + + + + + + - + .
+                               + + + + + - + + + + + + - + + .
+                               + + + + + + + + + + + - + + + .
+                               + - + + - + + + + + - + + + + .
+ +                             + + + + + + + + + - + + + + + .
+ +                             + + + - + + + + - + + + + + + .
+ +                             + + + + + + + - + + + + + + + .
- +                             - + - + + + - + + + + + + + - .
+ + +                           + + + + + - + + + + + + - + + .
+ - + +                         + - + + - + + + + + - + + + + .
+ + +   +                       + + + - + + + + - + + + + + + .
- + - + + +                     - + - + + + - + + + + + + + - .
+ - + + - + + + + +             + - + + - + + + + + - + + + + .
- + - + + + - + + + + + + +     - + - + + + - + + + + + + + - .

Видно, что в случаях а, б, в побеждает первый, а в случае г - второй игрок. При этом в первых двух пунктах первый игрок может придерживаться такой стратегии: всякий раз предлагать сопернику квадратную шоколадку. Для пункта в (5*15) такой принцип не пройдёт, нельзя сделать квадрат первым ходом. Поэтому первым ходом можно, например, оставить противнику шоколадку 5*11, а потом, в зависимости от его ответа, 2*11 или 5*5 и так далее.

Можно доказать (попробуйте это сделать самостоятельно), что при игре в шоколадку n*m (n<m) второй может гарантированно победить только при m=(n+1)*2^k-1, где k=0, 1, 2, 3, ..., а во всех иных случаях победит начинающий игру.

Игра N 4 ("крестики-нолики")

С этой игрой произошла неожиданность. Авторское решение задания было основано на центральной симметрии: второй игрок победит, обводя (то есть делая толстым) отрезок, симметричный относительно центра фигуры отрезку, обведённому первым игроком. При этом центральную клетку займут нолики (отчего и победят), а количество всех остальных ноликов будет равно количеству всех крестиков.

Однако несколько участников конкурса нашли иную, в каком-то смысле более сильную стратегию для второго игрока: он может на ходы первого отвечать симметрично относительно прямой, содержащей диагональ центральной клетки. В этом случае ноликам достаются целых 5 лишних клеток (те, что на этой прямой)!

Игра N 5 ("змейка").

Эта игра очень понравилась участникам, почти все упомянули её в работах. Многие поняли её как борьбу за территорию: "Надо отрезать противнику путь, и он замкнётся", "надо отрезать от противника бо'льшую часть доски". Победить в борьбе может второй игрок, руководствуясь всё той же симметричной стратегией: делая свой ход центрально-симметрично ходу соперника, он не нарушит правил, и последний ход будет за ним.

Игра N 6 (закрашивание клеток).

При описании стратегий в этой игре мы будем считать, что на игровом поле строчки не короче столбцов.

Игра на поле 2*n - это так называемая "игра-шутка": в ней исход игры предопределён и не зависит от ходов игроков. Ясно, что каждый ход производится в новый столбец; в любой нетронутый столбец пойти всегда может каждый игрок. Поэтому исход этой игры зависит только от чётности числа столбцов: при чётном n победит второй, а при нечётном n - первый игрок.

Игра на поле 3*n поначалу кажется несложной. Создаётся впечатление, что второй игрок побеждает, следуя простому правилу: отвечать в тот же столбец, куда ходил только что первый. Действительно, такой ход всегда возможен, всегда вынуждает первого игрока "открывать" новый столбец, но если следовать этой стратегии "бездумно", то в конце игры может возникнуть, например, такое положение:

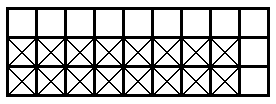
Первый может закрасить верхний правый угол и победить! Чтобы избежать такого исхода, второй игрок должен аккуратно разыграть эндшпиль: перед предпоследним ходом убедиться, что нет пустой строки, а если таковая есть, то закрасить свою клетку именно в ней. Тогда победа ему гарантирована.

В игре на поле 4*6 победит второй, придерживаясь центрально-симметричной стратегии. (Эта же стратегия позволяет выиграть второму игроку на любом поле, и длина, и ширина которого - чётные).

В общем случае m*n выигрышной стратегии для какого-либо из игроков авторы не знают.

Игра на поле 4*5 - достаточно простая для полного компьютерного перебора (написание соответствующей программы вполне по силам для школьника; обращаем ваше внимание на то, что игровая позиция по сути не меняется от перестановок строк и столбцов, этим можно воспользоваться для существенного сокращения вариантов перебора).

К сожалению, жюри Ломоносовского турнира не удалось придумать "некомпьютерное" решение, а также сформулировать достаточно простую, интересную и компактную (для публикации в этой книжке) выигрышную стратегию. Если вам удастся это сделать - очень хорошо. А пока эту игру можно использовать именно в качестве игры, а не математической задачи.

Игры N 1 и N 3 - математический фольклор (сами игры известны давно, а вот их авторы давно забыты); остальные игры предложили: N 2 - Александр Хачатурян, N 4 - Мария Ахмеджанова, N 5 - Александр Спивак, N 6 - Виктор Клепцын.

Критерии награждения