9 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Для каких значений x выполняется неравенство: 
?
1.2. Окружность пересекает оси координат в точках А(a; 0); B(b; 0); C(0;c) и D(0; d). Найдите координаты ее центра.
1.3. При каких натуральных n число n2 – 1 является степенью простого числа>?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Существует ли такое значение α, что все члены бесконечной последовательности cosα; cos2α; ... ; cos(2n;α); ... принимают отрицательные значения?
2.2. На каждой грани правильного тетраэдра с ребром 1 во внешнюю сторону построены правильные тетраэдры. Четыре их вершины, не принадлежащие исходному тетраэдру, образовали новый тетраэдр. Найдите его ребра.
2.3. Может ли объединение двух треугольников оказаться 13-угольником?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Сумма восьми чисел равна 
. Оказалось, что сумма любых семи чисел из этих восьми – положительна. Какое наименьшее целое значение может принимать наименьшее из данных чисел?
3.2. Дан четырехугольник АВСD площади 1. Из его внутренней точки О опущены перпендикуляры OK, OL, OM и ON на стороны АВ, ВС, CD и DA соответственно. Известно, что AK ≥ KB, BL ≥ LC, CM ≥ MD и DN ≥ NA. Найдите площадь четырехугольника KLMN.
3.3. В однокруговом турнире участвуют 10 шахматистов. Через какое наименьшее количество туров может оказаться так, что единоличный победитель уже выявился досрочно? (В каждом туре участники разбиваются на пары. Выигрыш – 1 очко; ничья – 0,5 очка; поражение – 0).
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Числа x, y, z и t лежат в интервале (0, 1). Докажите неравенство:
< 4 .
4.2. Известно, что в неравностороннем треугольнике ABC точка, симметричная точке пересечения медиан относительно стороны BC, принадлежит описанной окружности. Докажите, что ∠ BAC < 60°.
4.3. Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого из рыцарей ровно три врага, причём враги его друзей являются его врагами. При каких n такое возможно?
Пятый тур (15 минут; каждая задача – 7 баллов).
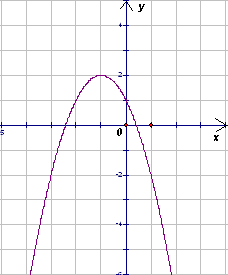5.1. На координатной плоскости изображен график функции y = ax2 + bx + c (см. рисунок). На этой же координатной плоскости схематически изобразите график функции y = cx2 + 2bx + a. Ответ поясните.
