11 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите систему: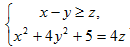 
1.2. Существует ли выпуклый 1000-угольник, у которого все углы выражаются целыми числами градусов?
1.3. ТСуществует ли такая цифра а, что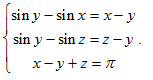 
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Числовая функция f такова, что для любых x и y выполняется равенство f(x + y) = f(x) + f(y) + 80xy. Найдите f(1), если f(0,25) = 2.
2.2. Четырёхугольник АВСD – вписанный. Лучи АВ и DС пересекаются в точке M, а лучи ВС и AD – в точке N. Известно, что ВМ = DN. Докажите, что CM = CN.
2.3. На доске размером 88 в углу расставлены 9 фишек в форме квадрата 33. Любая фишка может прыгать через другую фишку на свободную клетку (по горизонтали, вертикали или диагонали). Можно ли за некоторое количество прыжков расставить фишки в форме такого же квадрата в каком-либо другом углу доски?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Решите систему уравнений: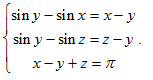
3.2. Точки D, Е и F – середины сторон ВС, АС и АВ треугольника АВС соответственно. Через центры вписанных окружностей треугольников AEF, BDF и СDE проведена окружность. Докажите, что ее радиус равен радиусу окружности, описанной около треугольника DEF.
3.3. На столе выложены в ряд 64 гирьки, причем масса двух любых соседних гирек отличается на 1 г. Требуется разложить гирьки на две кучки с равными массами и равным количеством гирь. Всегда ли это удастся?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Существуют ли такие две функции с наименьшими положительными периодами 2 и 6, что их сумма имеет наименьший положительный период 3?
4.2. В тетраэдре АВСD: АВ = 8, ВС = 10, АС = 12, BD = 15. Известно, что четыре отрезка, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противолежащие грани, пересекаются в одной точке. Найдите длины ребер DA и DC.
4.3. В равенстве х5 + 2x + 3 = pk числа х и k – натуральные. Может ли число р быть простым?
Пятый тур (15 минут; каждая задача – 7 баллов).
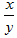, если 
