8 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Вася сложил четвертую степень и квадрат некоторого числа, отличного от нуля, и сообщил результат Пете. Сможет ли Петя однозначно определить Васино число?
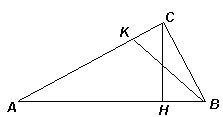
1.2. СВ прямоугольном треугольнике АВС проведена высота СН из вершины прямого угла. Из вершины В большего острого угла проведен отрезок BK так, что ∠ CBK = ∠ CАB (см. рисунок). Докажите, что СН делит BK пополам.
1.3. По окончании шахматного турнира Незнайка сказал: «Я набрал на 3,5 очка больше, чем потерял». Могут ли его слова быть правдой? (Победа – 1 очко, ничья – 1/2очка, поражение – 0.)
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Упростите выражение (избавьтесь от как можно большего количества знаков корней): 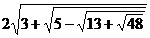 .
.
2.2. Бумажный прямоугольный треугольник АВС перегнули по прямой так, что вершина С прямого угла совместилась с вершиной В и получился четырехугольник. В каких отношениях точка пересечения диагоналей четырехугольника делит эти диагонали?
2.3. В клетках таблицы 3x3 расставили цифры от 1 до 9. Затем нашли суммы цифр в каждой строке. Какое наибольшее количество из этих сумм может оказаться полным квадратом?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Набор из нескольких чисел, среди которых нет одинаковых, обладает следующим свойством: среднее арифметическое каких-то двух чисел из этого набора равно среднему арифметическому каких-то трех чисел из набора и равно среднему арифметическому каких-то четырех чисел из набора. Каково наименьшее возможное количество чисел в таком наборе?
3.2. В треугольнике ABC на сторонах AB, AC и BC выбраны точки D, E и F соответственно так, что BF = 2CF, CE = 2AE и угол DEF – прямой. Докажите, что DE – биссектриса угла ADF.
3.3. На доске выписаны числа 1, 2, …, 100. На каждом этапе одновременно стираются все числа, не имеющие среди нестертых чисел делителей, кроме себя самого. Например, на первом этапе стирается только число 1. Какие числа будут стерты на последнем этапе?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Три числа x, y и z отличны от нуля и таковы, что x2 – y2 =yz и y2 – z2 =xz. Докажите, что x2 – z2 =xy.
4.2. В параллелограмме ABCDO – точка пересечения диагоналей. Точка M лежит на продолжении стороны AB за точку B. Известно, что угол AMO равен углу ВAD. Докажите, что MC = MD.
4.3. В ряд записаны 20 различных натуральных чисел. Произведение любых двух чисел, стоящих подряд, является квадратом натурального числа. Первое число равно 42. Докажите, что хотя бы одно из чисел больше, чем 16000.