11 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите уравнение: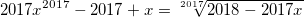 
1.2. В четырехугольнике ABCD: AB = ВС = m, ∠АВС = ∠АDС = 120°. Найдите BD.
1.3. В зале стоят шесть стульев в два ряда – по три стула в каждом, один ряд ровно за другим. В зал пришли шесть человек различного роста. Сколькими способами можно рассадить их так, чтобы каждый человек, сидящий в первом ряду, был ниже человека, сидящего за ним?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Какие значения может принимать выражение x+y+z, если sinx=cosy, siny=cosz, sinz=cosx, 0 ≤ x, y, z≤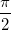 
2.2. Может ли квадрат являться разверткой треугольной пирамиды?
2.3. Из клетчатой доски размером 8×8 выпилили 8 прямоугольников размером 2×1. После этого из оставшейся части требуется выпилить квадрат размером 2×2. Обязательно ли это удастся?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Для всех действительных x и y выполняется равенство f(x2+y)=f(x)+f(y2). Найдите f(-1).
3.2. Пусть R1, R2 и R3 - радиусы трех окружностей, каждая из которых проходит через вершину треугольника и касается противолежащей стороны. Докажите, что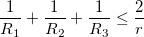 
, где r - радиус окружности, вписанной в этот треугольник.
3.3. Докажите, что среднее арифметическое всех делителей натурального числа n лежит на отрезке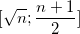 
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Известно, что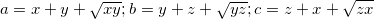 
, где x>0, y>0, z>0. Докажите, что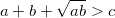 
4.2. В выпуклом четырехугольнике АВСD точка K – середина стороны ВС, а площадь треугольника AKD равна половине площади АВСD. Найдите длину медианы КЕ треугольника AKD, если AB = a, CD = b.
4.3. Можно ли на числовой прямой расположить три отрезка чётной длины так, чтобы общие части каждых двух из них были отрезками нечётной длины?
Пятый тур (15 минут; каждая задача – 7 баллов).
