10 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите систему уравнений: 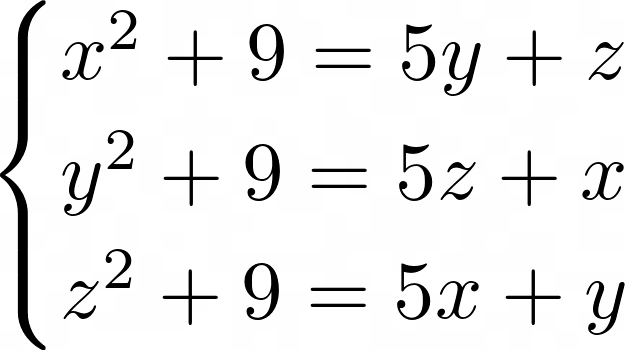
1.2. Один параллелограмм лежит внутри другого. Может ли сумма диагоналей внутреннего быть больше суммы диагоналей внешнего?
1.3. Можно ли расставить числа 1, 2, 3, 4, 5, 6, 7, 8 по кругу в таком порядке, чтобы каждое число делилось на разность своих соседей?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. На координатной плоскости постройте множество точек (x; y), для которых неравенство |xsinα + ycosα| ≤ 1 выполняется независимо от значения α.
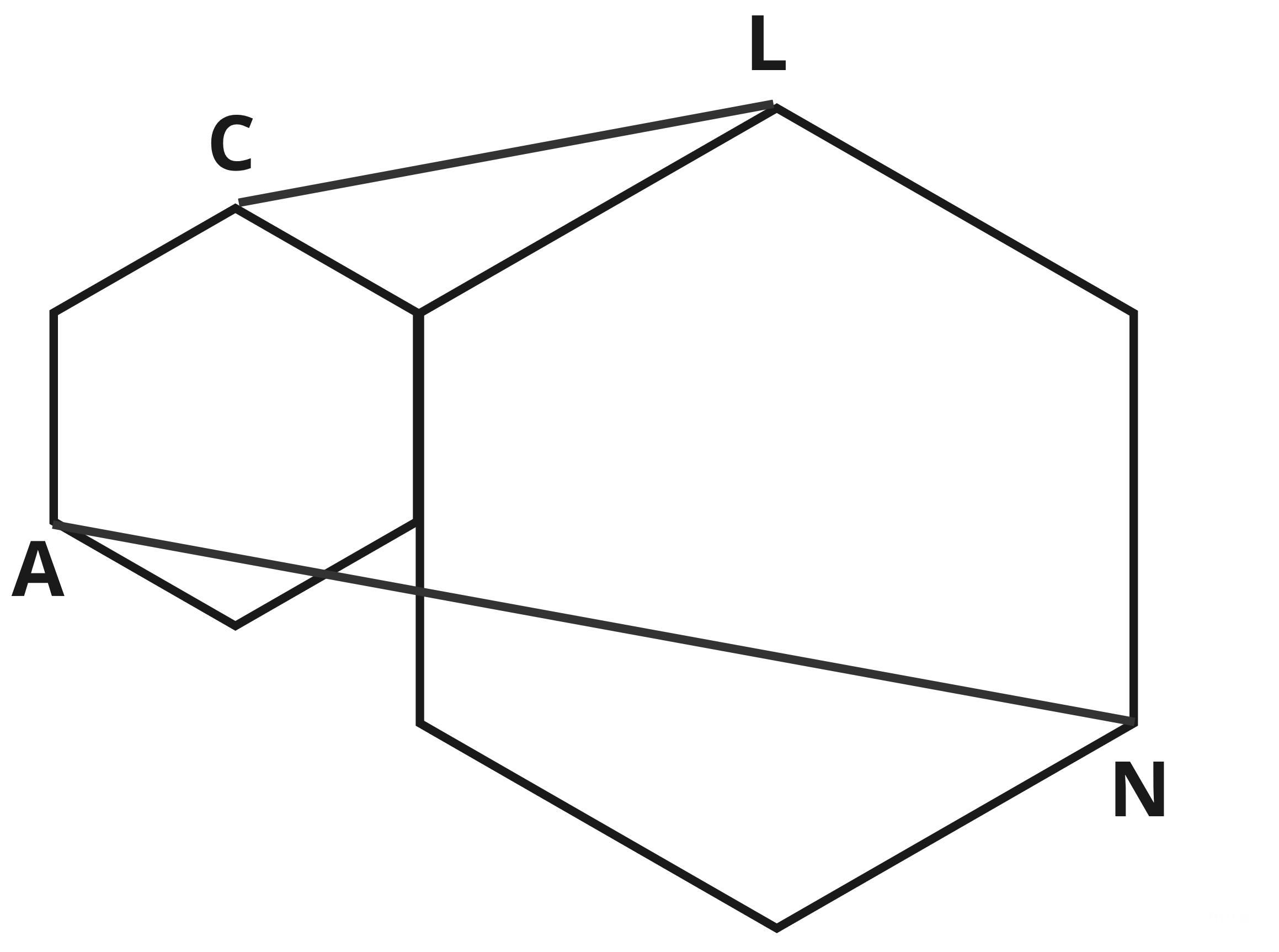
2.2. Два правильных шестиугольника с отношением сторон 1 : 2 расположены так, как показано на рисунке. Найдите АN, если CL = 6.
2.3. Можно ли раскрасить всю плоскость в два цвета – черный и белый – таким образом, чтобы на каждой окружности радиуса 1 лежали ровно две белые точки?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Можно ли число 1111111122222222 (восемь единиц и восемь двоек) представить в виде произведения двух последовательных натуральных чисел?
3.2. Найдите наибольшую возможную площадь ортогональной проекции правильного тетраэдра с ребром 1 на плоскость.
3.3. Рассматриваются все последовательности длины 8, составленные из чисел 1, 0 и –1. У скольких из них сумма всех членов равна нулю?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Найдите все такие функции, определённые на R, что для всех x и y выполняется равенство f(x + y + f(x)) = f(x + y) + yf(x).
4.2. В треугольнике ABC угол ACB равен 120°, M – середина AB. На сторонах AC и BC отмечены точки P и Q соответственно так, что AP = PQ = QB. Найдите угол PMQ.
4.3. Петя записал в ряд n чисел, каждое из которых 1 или –1 (n > 4). Каждым вопросом Вася может узнать у него произведение любых трёх чисел. За какое наименьшее количество вопросов он сможет узнать произведение всех чисел, написанных Петей?
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. В школе 1000 школьников и 35 классов. Каждому школьнику на лбу написали, сколько в его классе учеников. Чему может равняться сумма чисел, обратных записанным?
5.2. В остроугольном треугольнике АВС: ВМ – медиана, Н – ортоцентр, Р – основание перпендикуляра, опущенного из Н на ВМ. Докажите, что ВM·МР = АМ2.
5.3. Найдите все такие натуральные числа m и n, где m > n, что m!·n! = 10!
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | 5 тур | Сумма | Диплом | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| Жуковский А | 6 | 6 | 6 | 6 | 7 | 7 | 8 | 4 | 8 | 9 | 9 | 9 | 7 | 7 | 7 | 106 | I |
| 2 0 8 6 А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 1 | 9 | 9 | 7 | 7 | 7 | 103 | I |
| 1 5 1 4 Г | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 1 | 9 | 3 | 7 | 0 | 7 | 90 | II |
| 2 0 8 6 Б | 4 | 6 | 6 | 7 | 7 | 7 | 4 | 2 | 6 | 9 | 9 | 2 | 7 | 7 | 7 | 90 | II |
| Ц П М А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 0 | 8 | 1 | 9 | 0 | 7 | 7 | 7 | 86 | II |
| 5 7 Г | 3 | 0 | 6 | 7 | 7 | 7 | 0 | 8 | 8 | 0 | 9 | 0 | 7 | 7 | 7 | 76 | III |
| ФМШ В Тюмень | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 0 | 8 | 1 | 0 | 4 | 7 | 7 | 7 | 73 | III |
| 1 7 9 Б | 4 | 6 | 6 | 7 | 7 | 5 | 0 | 4 | 8 | 0 | 9 | 4 | 7 | 0 | 5 | 72 | III |
| 1 7 9 А | 4 | 6 | 6 | 0 | 7 | 7 | 0 | 2 | 8 | 1 | 9 | 7 | 7 | 0 | 7 | 71 | III |
| 1 5 1 4 А | 4 | 6 | 6 | 0 | 7 | 7 | 0 | 1 | 8 | 0 | 9 | 6 | 7 | 0 | 7 | 68 | III |
| 3 1 5 А | 6 | 0 | 6 | 0 | 5 | 7 | 8 | 0 | 8 | 1 | 0 | 5 | 7 | 7 | 7 | 67 | III |
| 5 А Долгопрудный | 6 | 0 | 6 | 7 | 7 | 7 | 0 | 0 | 8 | 0 | 0 | 3 | 7 | 7 | 7 | 65 | III |
| В Ш Э Е | 4 | 0 | 6 | 0 | 7 | 6 | 0 | 0 | 8 | 0 | 9 | 2 | 7 | 7 | 7 | 63 | III |
| 4 4 4 А | 0 | 0 | 6 | 0 | 7 | 7 | 0 | 3 | 6 | 1 | 9 | 1 | 7 | 7 | 7 | 61 | ПП |
| Л 2 Ш Б | 6 | 0 | 0 | 0 | 7 | 7 | 8 | 0 | 6 | 2 | 0 | 4 | 7 | 7 | 7 | 61 | ПП |
| Ц П М Б | 0 | 6 | 6 | 0 | 0 | 7 | 0 | 0 | 8 | 0 | 9 | 4 | 7 | 7 | 7 | 61 | ПП |
| В Ш Э В | 4 | 6 | 6 | 1 | 7 | 7 | 0 | 0 | 8 | 1 | 0 | 6 | 7 | 0 | 7 | 60 | ПП |
| 4 4 4 В | 1 | 5 | 6 | 7 | 7 | 7 | 0 | 2 | 8 | 0 | 1 | 1 | 7 | 0 | 7 | 59 | |
| 1 7 1 Б | 2 | 0 | 6 | 7 | 7 | 7 | 8 | 0 | 0 | 0 | 0 | 0 | 7 | 7 | 7 | 58 | |
| 2 0 0 7 Ж | 6 | 0 | 6 | 6 | 7 | 7 | 0 | 1 | 0 | 0 | 7 | 4 | 7 | 0 | 7 | 58 | |
| М И Ф И Б | 0 | 0 | 6 | 6 | 7 | 7 | 4 | 5 | 6 | 0 | 0 | 6 | 3 | 1 | 7 | 58 | |
| 5 7 Б | 1 | 0 | 6 | 7 | 7 | 7 | 0 | 0 | 6 | 1 | 0 | 4 | 7 | 0 | 7 | 53 | |
| 2 2 4 Б | 0 | 0 | 6 | 1 | 7 | 7 | 0 | 8 | 8 | 0 | 0 | 3 | 7 | 0 | 6 | 53 | |
| 1 4 1 6 А | 0 | 0 | 6 | 1 | 7 | 7 | 0 | 0 | 8 | 0 | 9 | 1 | 7 | 0 | 7 | 53 | |
| В Ш Э Д | 0 | 0 | 6 | 0 | 7 | 7 | 4 | 0 | 8 | 1 | 0 | 6 | 7 | 0 | 7 | 53 | |
| 1 5 5 7 А | 4 | 6 | 6 | 1 | 0 | 7 | 8 | 0 | 0 | 0 | 7 | -1 | 7 | 0 | 7 | 52 | |
| 38 А Н. Новгород | 6 | 5 | 6 | 6 | 5 | 0 | 0 | 0 | 4 | 1 | 2 | 2 | 7 | 0 | 7 | 51 | |
| 5 7 А | 0 | 0 | 0 | 4 | 7 | 7 | 0 | 0 | 6 | 1 | 1 | 9 | 7 | 0 | 7 | 49 | |
| Ц П М Д | 1 | 0 | 0 | 1 | 7 | 7 | 0 | 0 | 8 | 1 | 0 | 1 | 7 | 7 | 7 | 47 | |
| 1 7 1 В | 2 | 0 | 6 | 2 | 5 | 7 | 1 | 2 | 8 | 2 | 0 | 0 | 7 | 1 | 2 | 45 | |
| ФМШ З Тюмень | 4 | 0 | 6 | 0 | 7 | 7 | 0 | 0 | 8 | 0 | 0 | 5 | 7 | 0 | 0 | 44 | |
| М И Ф И А | 1 | 0 | 0 | 7 | 7 | 0 | 0 | 1 | 0 | 9 | 2 | 2 | 7 | 0 | 7 | 43 | |
| ФМШ Г Тюмень | 0 | 0 | 6 | 0 | 7 | 7 | 0 | 7 | 8 | 0 | 0 | 1 | 0 | 0 | 7 | 43 | |
| 2 0 0 7 А | 4 | 0 | 0 | 1 | 0 | 7 | 0 | 0 | 8 | 0 | 0 | 6 | 7 | 2 | 7 | 42 | |
| 1 7 9 В | 4 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 6 | 0 | 1 | 2 | 7 | 1 | 7 | 41 | |
| 1 5 1 4 Б | 1 | 6 | 6 | 1 | 7 | 7 | 0 | 2 | 1 | 0 | 0 | 1 | 7 | 0 | 1 | 40 | |
| 2 0 0 7 Б | 4 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 4 | 0 | 0 | 5 | 7 | 0 | 7 | 40 | |
| 5 7 В | 4 | 0 | 6 | 6 | 7 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 7 | 38 | |
| В Ш Э Г | 4 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 8 | 0 | 0 | 1 | 7 | 0 | 1 | 34 | |
| 1 3 7 0 Б | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 8 | 0 | 9 | 0 | 7 | 3 | 1 | 33 | |
| Л Н И П А | 0 | 0 | 6 | 3 | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 7 | 0 | 7 | 30 | |
| 2 0 5 1 А | 4 | 6 | 6 | -1 | 0 | 0 | 4 | 0 | 6 | 0 | 0 | 1 | 0 | 0 | 2 | 28 | |
| 6 4 А | 4 | 0 | 6 | 6 | 5 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 27 | |
| 1 3 7 1 А | 1 | 0 | 6 | 0 | 0 | 0 | 8 | 0 | 0 | 1 | 0 | 1 | 7 | 0 | 3 | 27 | |
| 2 0 0 7 З | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 7 | 0 | 7 | 24 | |
| Ч у й к о в а А | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 7 | 0 | 7 | 24 | |
| Ц П М Г | 1 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 8 | 1 | 0 | 0 | 0 | 0 | 7 | 23 | |
| 1 3 7 0 А | 0 | 0 | 6 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 7 | 0 | 1 | 22 | |
| 2 0 3 3 А | 1 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 7 | 22 | |
| 2 0 3 3 Б | 4 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 7 | 22 | |
| 2 0 3 6 А | 0 | 0 | 0 | 1 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 1 | 7 | 0 | 7 | 20 | |
| 2 2 4 А | 1 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 15 | |
| 2 9 3 А | 0 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 15 | |
| 2 1 0 7 А | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 7 | 0 | 1 | 15 | |
| 1 3 7 1 Б | 0 | 0 | 6 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 12 | |
| 2 9 3 Б | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 8 | |
| 1 2 3 1 Б | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 8 | |
| 2 0 0 5 А | 0 | 0 | 0 | 1 | 1 | 0 | 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 1 8 7 4 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |