8 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите уравнение: 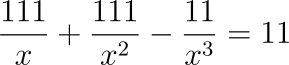
1.2. Вершину A прямоугольника ABCD соединили отрезками с серединами сторон BC и CD. Мог ли один из этих отрезков оказаться вдвое длиннее другого?
1.3. К некоторому натуральному числу прибавили удвоенную сумму его цифр. Могло ли получиться число 2024?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Однажды 91 участник летнего лагеря решили сходить в кино. Прошлым летом они бы поместились в 8 рядов кинозала (но не в 7). Однако этим летом каждое четвёртое кресло (то есть каждое кресло, номер которого в ряду делится на 4) должно оставаться пустым, поэтому один участник не поместился в кинозале. Сколько рядов в зале и сколько кресел в каждом из них, если во всех рядах поровну мест?
2.2. На сторонах CD и AD квадрата ABCD отмечены точки K и М так, что MK = CK. Перпендикуляр к MK, проходящий через точку М, пересекает АВ в точке N. Докажите, что расстояние от С до прямой MN равно стороне квадрата.
2.3. В комнате находятся несколько рыцарей и лжецов (рыцари всегда говорят правду, а лжецы всегда лгут). Каждому дали листок бумаги и попросили написать про каждого из остальных, кем он является: лжецом или рыцарем. Когда собрали все листы и произвели подсчёты, то записей «лжец» оказалось 40, а записей «рыцарь» – 32. Сколько в комнате рыцарей, если известно, что их больше, чем лжецов?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Докажите, что число 2022·20243 – 2023·20213 является кубом целого числа.
3.2. Дан квадрат со стороной 1. Найдите геометрическое место точек, для которых сумма расстояний до прямых, содержащих его стороны, равна 4.
3.3. В клетках прямоугольной таблицы расставлены натуральные числа так, что в каждой строчке и в каждом столбце сумма чисел чётна. Докажите, что, если раскрасить клетки таблицы в шахматном порядке, то сумма чисел в чёрных клетках будет чётна.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Можно ли сократить дробь 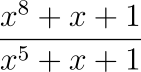 на многочлен ненулевой степени с целыми коэффициентами?
на многочлен ненулевой степени с целыми коэффициентами?
4.2. В треугольнике АВС проведена медиана ВМ. Найдите угол АВМ, если ∠ВАС = 30°, ∠ВСА = 105°.
4.3. На некоторой планете между тремя городами A, B и C проложены дороги так, что каждый город связан с каждым больше, чем одной дорогой. Назовем путём из одного города в другой любой способ проехать напрямую или через третий город. Известно, что города A и B связывают 29 путей, а города B и C – 23 пути. Сколько путей связывают города A и C? (Движение по всем дорогам двустороннее.)
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | Сумма | Диплом | ||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| 1 7 9 Б | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 90 | I |
| В Г Г | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 90 | I |
| Л 2 Ш М | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 90 | I |
| 2 0 0 7 Ч | 6 | 6 | 6 | 4 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 87 | I |
| Раз-два-три Б | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 6 | 9 | 0 | 9 | 79 | II |
| Ф М Ш Б Тюмень | 6 | 6 | 6 | 5 | 7 | 7 | 8 | 6 | 0 | 9 | 9 | 9 | 78 | II |
| 2 0 0 7 К | 6 | 0 | 6 | 7 | 7 | 7 | 8 | 8 | 0 | 9 | 9 | 9 | 76 | II |
| Раз-два-три А | 0 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 0 | 9 | 75 | II |
| 5 В Долгопрудный | 0 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 0 | 9 | 9 | 7 | 74 | II |
| 2 0 0 7 М | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 0 | 9 | 1 | 9 | 74 | II |
| 4 4 4 Б | 6 | 6 | 0 | 7 | 7 | 7 | 8 | 4 | 0 | 9 | 9 | 9 | 72 | II |
| Л 2 Ш Ж | 0 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 0 | 9 | 9 | 4 | 71 | II |
| Ф Т Ш Б СПб | 0 | 6 | 6 | 7 | 7 | 7 | 8 | 2 | 0 | 9 | 9 | 9 | 70 | II |
| Л 2 Ш И | 0 | 6 | 0 | 7 | 7 | 7 | 8 | 8 | 0 | 9 | 9 | 4 | 65 | III |
| 4 4 4 А | 0 | 4 | 6 | 5 | 7 | 7 | 0 | 8 | 0 | 9 | 9 | 9 | 64 | III |
| 5 Б Долгопрудный | 6 | 6 | 6 | 7 | 7 | 5 | 0 | 8 | 0 | 0 | 9 | 9 | 63 | III |
| Л 2 Ш К | 6 | 6 | 6 | 5 | 7 | 7 | 0 | 6 | 6 | 9 | 0 | 4 | 62 | III |
| Ф М Ш З Тюмень | 6 | 7 | 7 | 7 | 8 | 7 | 0 | 0 | 9 | 9 | 60 | III | ||
| Летово Н | 6 | 6 | -1 | 7 | 7 | 7 | 8 | 8 | 0 | 0 | 0 | 7 | 55 | ПП |
| 2 1 8 А | 6 | 6 | 6 | 3 | 7 | 6 | 8 | 4 | 0 | 0 | 6 | 2 | 54 | |
| 2 0 0 7 Х | 0 | 6 | 6 | 5 | 0 | 7 | 8 | 5 | 8 | 0 | 0 | 9 | 54 | |
| Интеллектуал Б | 0 | 6 | 6 | 5 | 7 | 4 | 0 | 8 | 0 | 0 | 9 | 9 | 54 | |
| Ф М Ш В Тюмень | 0 | 0 | 6 | 7 | 7 | 0 | 8 | 8 | 0 | 0 | 9 | 9 | 54 | |
| 1 7 1 В | 0 | 6 | 6 | 7 | 7 | 7 | 8 | 2 | 0 | 0 | 1 | 9 | 53 | |
| 1 5 4 3 Б | 0 | 6 | 6 | 7 | 7 | 1 | 8 | 2 | 2 | 0 | 9 | 4 | 52 | |
| 1 5 4 3 В | 6 | 6 | 6 | 0 | 7 | 7 | 8 | 8 | 0 | 0 | 0 | 4 | 52 | |
| Летово Е | 6 | 0 | 6 | 7 | 7 | 7 | 0 | 8 | 0 | 0 | 1 | 9 | 51 | |
| Сигма А | 0 | 0 | 6 | 7 | 7 | 7 | 8 | 8 | 0 | 0 | 0 | 6 | 49 | |
| Летово Г | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 8 | 0 | 0 | 0 | 0 | 47 | |
| 1 7 9 В | 0 | 6 | 6 | 7 | 0 | 7 | 0 | 8 | 0 | 9 | 0 | 2 | 45 | |
| В Г В | 0 | 6 | 6 | 5 | 7 | 7 | 0 | 5 | 0 | 0 | 0 | 9 | 45 | |
| 5 4 8 Б | 6 | 4 | 6 | 7 | 7 | 5 | 8 | 0 | 0 | 0 | 1 | 0 | 44 | |
| 1 5 4 3 А | 3 | 6 | 0 | 0 | 7 | 2 | 0 | 8 | 0 | 0 | 9 | 8 | 43 | |
| 1 5 4 7 Г | 6 | 0 | 6 | 3 | 7 | 7 | 8 | 4 | 0 | 0 | 1 | 0 | 42 | |
| Ш Ц П М А | 0 | 6 | 6 | 7 | 3 | 7 | 0 | 2 | 0 | 0 | 1 | 9 | 41 | |
| Ш Ц П М Б | 0 | 0 | 6 | 7 | 7 | 3 | 0 | 0 | 0 | 0 | 9 | 9 | 41 | |
| Ш Ц П М Г | 6 | 6 | 6 | 7 | 0 | 4 | 0 | 8 | 0 | 0 | 0 | 4 | 41 | |
| 2 0 8 6 Д | 0 | 0 | 6 | 7 | 7 | 7 | 0 | 4 | 0 | 0 | 9 | 0 | 40 | |
| 1 5 3 7 Б | 6 | 0 | 6 | 7 | 0 | 3 | 8 | 0 | 0 | 0 | 9 | 0 | 39 | |
| 5 8 А | 6 | 0 | 0 | 5 | 6 | 7 | 8 | 4 | 0 | 0 | 0 | 2 | 38 | |
| 5 4 8 Д | 0 | 6 | 6 | 0 | 7 | 1 | 0 | 6 | 0 | 0 | 1 | 9 | 36 | |
| 2 1 8 Б | 6 | 0 | 0 | 7 | 7 | 7 | 8 | 0 | 0 | 0 | 0 | 0 | 35 | |
| Ф М Ш И Тюмень | 0 | 0 | 6 | 0 | 7 | 4 | 0 | 0 | 9 | 9 | 35 | |||
| Ш Ц П М В | 0 | 0 | 6 | 7 | 7 | 7 | 8 | 0 | 0 | 0 | 0 | 0 | 35 | |
| 1 А Фрязино | 0 | 6 | 6 | 5 | 0 | 5 | 0 | 0 | 0 | 1 | 9 | 32 | ||
| 1 5 3 4 А | 0 | 0 | 6 | 7 | 7 | 8 | 4 | 0 | 0 | 0 | 0 | 32 | ||
| 5 7 А | 0 | 6 | 6 | 0 | 7 | 7 | 0 | 0 | 0 | 0 | 0 | 5 | 31 | |
| 1 3 5 9 Б | 0 | 0 | 0 | 7 | 7 | 5 | 0 | 0 | 0 | 0 | 9 | 3 | 31 | |
| 1 7 1 Ж | 0 | 6 | 0 | 3 | 0 | 7 | 8 | 4 | 0 | 0 | 0 | 2 | 30 | |
| Летово М | 0 | 6 | 6 | 7 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 7 | 29 | |
| Примакова А | 0 | 0 | 6 | 5 | 0 | 5 | 8 | 2 | 0 | 0 | 0 | 0 | 26 | |
| 1 7 1 Е | 0 | 0 | 6 | 7 | 7 | 5 | 0 | -1 | 0 | 0 | 0 | 0 | 24 | |
| 1 3 5 7 А | 0 | 0 | 6 | 0 | 3 | 5 | 0 | 0 | 0 | 0 | 0 | 9 | 23 | |
| 1 3 5 3 А | 0 | 0 | 0 | 3 | 7 | 3 | 0 | 0 | 0 | 0 | 9 | 0 | 22 | |
| 1 3 6 3 В | 0 | 0 | 0 | 3 | 0 | 6 | 0 | 4 | 0 | 0 | 0 | 9 | 22 | |
| 1 5 1 1 В | 0 | 6 | 0 | 0 | 7 | 3 | 0 | 4 | 0 | 0 | 0 | 2 | 22 | |
| 1 5 8 0 Ж | 0 | 6 | 0 | 0 | 7 | 3 | 0 | 0 | 0 | 1 | 2 | 19 | ||
| Т Г У Б Тюмень | 0 | 6 | 6 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | |
| Интеллектуал А | 0 | 0 | 6 | 5 | 0 | 1 | 0 | 4 | 0 | 0 | 0 | 2 | 18 | |
| 1 8 1 1 А | 0 | 0 | 0 | 7 | 0 | 3 | 0 | 5 | 0 | 0 | 0 | 1 | 16 | |
| 1 7 1 Д | 0 | 1 | 0 | 0 | 0 | 3 | 8 | 0 | 0 | 0 | 1 | 0 | 13 | |
| 5 4 8 А | 0 | 0 | 0 | 7 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 2 | 13 | |
| 1 6 0 1 А | 0 | 0 | 6 | 5 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | |
| 1 3 6 3 А | 0 | 0 | 0 | 3 | 7 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | |
| 1 5 1 1 А | 0 | 0 | 6 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | ||
| 1 5 1 1 Б | 0 | 6 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | |
| Т Г У А Тюмень | 0 | 0 | 6 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | |||
| 9 2 2 А | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 2 1 2 0 А | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | ||
| Золотое сечение А | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | |
| 1 5 7 5 Б | 0 | 0 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | |