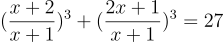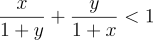Математическая регата 9 классов 12.10.2024
Задания | Результаты | Решения (doc-файл) | Решения (pdf-файл)
9 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите уравнение: 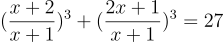
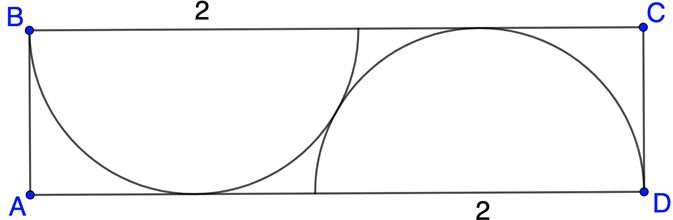
1.2. Внутри прямоугольника расположены две полуокружности диаметра 2, каждая из которых касается другой
полуокружности и двух сторон прямоугольника (см. рисунок). Найдите длину его диагонали.
1.3. Можно ли, используя только цифры 2, 3, 4, 9, составить два натуральных числа, одно из которых в 19 раз больше другого?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Пусть а, b и с – попарно различные числа. Докажите, что a2(c – b) + b2(a – c) + c2(b – a) не равно нулю.
2.2. Докажите, что с помощью трёх одинаковых кругов радиуса 1 можно покрыть любой прямоугольный треугольник с гипотенузой 4.
2.3. На доске записаны числа 5 и 8. За один ход можно либо увеличить оба числа на 1, либо разделить на их общий натуральный делитель. Можно ли за несколько ходов добиться того, что на доске будут записаны числа 5 и 3?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Крокодил переплыл реку за 6 минут. Он плыл перпендикулярно берегам, но течением его снесло на половину ширины реки. За какое время он сможет приплыть обратно в точку старта?
3.2. На стороне АС равностороннего треугольника АВС как на диаметре построена полуокружность вне треугольника.
На этой полуокружности отмечены точки K и L, которые делят её на три равные дуги.
Докажите, что точки пересечения BK и BL со стороной АС делят эту сторону на три равные части.
3.3. В шахматном круговом турнире 8 участников, из которых четверо выходят в финал. Какое наименьшее количество очков гарантирует шахматисту выход в финал? Каждый участник играет с каждым один раз, победа – 1 очко, ничья – 0,5, поражение – 0.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Представьте число 989·1001·1007 + 320 в виде произведения трёх натуральных множителей, каждый из которых больше 1.
4.2. Через точку М, лежащую внутри окружности и отличную от её центра, проведены три хорды так, что угол между каждыми
двумя соседними равен 60°. Образовалось шесть отрезков, у которых один конец лежит на окружности, а другой – в точке М.
Докажите, что сумма длин трёх отрезков, взятых через один, равна сумме длин других трёх отрезков.
4.3. На клетчатой плоскости отметили 14 клеток. Обязательно ли найдётся клетчатый прямоугольник, содержащий ровно 7 отмеченных клеток?
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Докажите, что для любых x и y из интервала (0; 1) выполняется неравенство 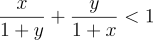
5.2. В выпуклом шестиугольнике равны три пары противолежащих углов. Верно ли, что в нём есть параллельные стороны?
5.3. Поверхность куба полностью окрашена. Его распилили на несколько одинаковых кубиков. Оказалось, что количество вовсе неокрашенных кубиков равно количеству кубиков, у которых окрашена ровно одна грань. На какое количество кубиков был распилен куб?
Результаты регаты:
| Команда |
1 тур |
2 тур |
3 тур |
4 тур |
5 тур |
Сумма |
Диплом |
| 1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
|
| 2 0 0 7 А |
6 |
6 |
6 |
7 |
7 |
7 |
8 |
8 |
8 |
9 |
0 |
0 |
7 |
7 |
7 |
93 |
I
|
| Новаторы А |
6 |
6 |
6 |
7 |
7 |
7 |
8 |
8 |
8 |
9 |
0 |
0 |
7 |
7 |
7 |
93 |
I
|
| 1 7 9 В |
6 |
3 |
6 |
7 |
7 |
7 |
8 |
8 |
8 |
9 |
0 |
0 |
7 |
7 |
7 |
90 |
I
|
| 5 3 3 Б СПб |
1 |
6 |
6 |
7 |
7 |
7 |
8 |
8 |
8 |
9 |
0 |
0 |
7 |
7 |
7 |
88 |
II
|
| Летово З |
6 |
0 |
6 |
7 |
7 |
7 |
0 |
8 |
8 |
9 |
8 |
0 |
7 |
7 |
7 |
87 |
II
|
| Ф Т Ш З СПб |
6 |
6 |
6 |
7 |
7 |
7 |
0 |
8 |
8 |
9 |
0 |
0 |
7 |
7 |
7 |
85 |
II
|
| 2 0 0 7 Я |
6 |
6 |
6 |
7 |
7 |
7 |
8 |
8 |
8 |
0 |
0 |
0 |
7 |
7 |
7 |
84 |
II
|
| Л 2 Ш Н |
6 |
6 |
6 |
3 |
7 |
7 |
8 |
8 |
8 |
9 |
0 |
0 |
0 |
7 |
6 |
81 |
II
|
| 3 6 6 Д СПб |
6 |
6 |
6 |
7 |
7 |
7 |
8 |
8 |
4 |
0 |
-1 |
0 |
7 |
7 |
7 |
79 |
II
|
| Л 2 Ш М |
1 |
6 |
6 |
7 |
7 |
7 |
8 |
8 |
8 |
0 |
0 |
0 |
7 |
7 |
7 |
79 |
II
|
| Л 2 Ш Л |
6 |
6 |
6 |
7 |
7 |
7 |
0 |
0 |
8 |
9 |
0 |
0 |
7 |
7 |
6 |
76 |
III
|
| В Г В |
6 |
4 |
6 |
7 |
7 |
7 |
0 |
8 |
8 |
0 |
2 |
0 |
6 |
7 |
7 |
75 |
III
|
| Ф М Ш Г Тюмень |
6 |
0 |
6 |
7 |
7 |
7 |
4 |
8 |
0 |
9 |
0 |
0 |
7 |
7 |
7 |
75 |
III
|
| 1 7 9 Г |
0 |
6 |
6 |
0 |
7 |
7 |
8 |
8 |
1 |
9 |
0 |
0 |
7 |
7 |
5 |
71 |
III
|
| 1 5 4 3 Б |
6 |
1 |
6 |
7 |
7 |
7 |
8 |
8 |
0 |
0 |
0 |
0 |
7 |
7 |
7 |
71 |
III
|
| Новаторы Б |
6 |
0 |
6 |
7 |
7 |
7 |
0 |
8 |
8 |
0 |
0 |
0 |
7 |
7 |
7 |
70 |
III
|
| К Ф М Л В Киров |
6 |
6 |
6 |
7 |
1 |
7 |
8 |
0 |
8 |
0 |
0 |
0 |
4 |
7 |
7 |
67 |
ПП
|
| 1 5 2 3 А |
2 |
6 |
6 |
7 |
7 |
4 |
0 |
8 |
0 |
9 |
0 |
0 |
7 |
7 |
0 |
63 |
ПП
|
| 1 5 4 3 В |
0 |
4 |
6 |
0 |
7 |
7 |
0 |
8 |
8 |
3 |
6 |
0 |
0 |
7 |
7 |
63 |
ПП
|
| Ф М Ш Е Тюмень |
0 |
6 |
6 |
7 |
7 |
7 |
0 |
8 |
0 |
0 |
0 |
0 |
7 |
7 |
7 |
62 |
ПП
|
| 1 7 9 А |
6 |
0 |
6 |
0 |
7 |
7 |
8 |
0 |
8 |
0 |
0 |
0 |
7 |
7 |
5 |
61 |
ПП
|
| Сигма А |
6 |
6 |
6 |
0 |
7 |
7 |
0 |
8 |
4 |
0 |
0 |
0 |
0 |
7 |
7 |
58 |
|
| 2 0 0 7 У |
6 |
0 |
0 |
0 |
7 |
7 |
8 |
8 |
0 |
0 |
0 |
0 |
7 |
7 |
7 |
57 |
|
| 1 7 1 В |
6 |
6 |
6 |
7 |
0 |
7 |
0 |
0 |
0 |
9 |
0 |
0 |
7 |
7 |
1 |
56 |
|
| 1 7 1 Д |
0 |
6 |
6 |
0 |
7 |
7 |
8 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
7 |
55 |
|
| 2 1 8 Б |
6 |
2 |
6 |
7 |
7 |
7 |
0 |
0 |
1 |
0 |
0 |
0 |
7 |
7 |
5 |
55 |
|
| Летово И |
3 |
6 |
6 |
7 |
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
5 |
55 |
|
| 1 7 1 Ж |
6 |
6 |
6 |
0 |
7 |
7 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
54 |
|
| 1 5 1 4 Е |
6 |
6 |
6 |
7 |
0 |
7 |
0 |
0 |
8 |
0 |
0 |
0 |
7 |
0 |
7 |
54 |
|
| Ш Ц П М И |
6 |
0 |
6 |
7 |
0 |
7 |
8 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
5 |
53 |
|
| 5 3 3 А СПб |
0 |
0 |
6 |
0 |
7 |
7 |
8 |
8 |
2 |
0 |
0 |
0 |
0 |
7 |
7 |
52 |
|
| Л 2 Ш И |
0 |
3 |
6 |
0 |
7 |
7 |
8 |
0 |
1 |
0 |
0 |
0 |
4 |
7 |
7 |
50 |
|
| Летово Е |
0 |
6 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
9 |
0 |
0 |
7 |
7 |
7 |
49 |
|
| 5 8 А |
0 |
0 |
6 |
0 |
4 |
0 |
8 |
8 |
0 |
0 |
0 |
0 |
7 |
7 |
7 |
47 |
|
| Ф Т Ш Ж СПб |
6 |
6 |
6 |
0 |
7 |
7 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
47 |
|
| 2 0 0 7 Т |
0 |
6 |
6 |
0 |
7 |
7 |
0 |
8 |
0 |
0 |
0 |
0 |
7 |
0 |
5 |
46 |
|
| Интеллектуал А |
3 |
6 |
6 |
0 |
7 |
7 |
2 |
7 |
0 |
0 |
0 |
0 |
0 |
7 |
1 |
46 |
|
| Ф М Ш Д Тюмень |
6 |
0 |
6 |
0 |
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
6 |
46 |
|
| Ш Ц П М Б |
6 |
6 |
6 |
7 |
7 |
5 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
45 |
|
| 2 1 8 В |
0 |
3 |
6 |
0 |
6 |
7 |
0 |
0 |
8 |
0 |
0 |
0 |
7 |
0 |
7 |
44 |
|
| Ф М Ш В Тюмень |
2 |
6 |
0 |
0 |
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
7 |
43 |
|
| 1 5 3 4 А |
0 |
0 |
6 |
7 |
0 |
7 |
8 |
0 |
0 |
9 |
0 |
0 |
0 |
0 |
5 |
42 |
|
| Летово К |
3 |
6 |
6 |
0 |
7 |
3 |
0 |
0 |
3 |
0 |
0 |
0 |
7 |
0 |
7 |
42 |
|
| Н П А Тюмень |
0 |
6 |
6 |
0 |
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
1 |
41 |
|
| 1 1 9 4 Г |
6 |
4 |
6 |
0 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
5 |
39 |
|
| В Г Б |
6 |
0 |
0 |
0 |
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
5 |
39 |
|
| Покровский кв. А |
0 |
0 |
6 |
0 |
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
5 |
39 |
|
| 1 3 6 3 А |
0 |
6 |
0 |
0 |
7 |
5 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
7 |
5 |
38 |
|
| 1 5 1 1 Б |
6 |
6 |
6 |
0 |
0 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
7 |
5 |
38 |
|
| 1 5 4 7 В |
0 |
0 |
6 |
0 |
0 |
7 |
0 |
0 |
6 |
9 |
0 |
0 |
3 |
0 |
7 |
38 |
|
| 1 5 8 0 Ж |
3 |
6 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
1 |
37 |
|
| 1 6 0 1 А |
6 |
0 |
6 |
0 |
2 |
7 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
0 |
7 |
37 |
|
| В Ш Э А |
0 |
0 |
6 |
0 |
7 |
7 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
7 |
0 |
36 |
|
| 1 5 8 0 О |
0 |
0 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
7 |
5 |
32 |
|
| 1 5 3 4 В |
6 |
6 |
0 |
0 |
6 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
5 |
31 |
|
| 1 5 1 1 В |
0 |
0 |
0 |
0 |
7 |
7 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
7 |
0 |
29 |
|
| 1 5 5 7 К |
3 |
0 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
5 |
28 |
|
| 1 5 5 7 Л |
3 |
6 |
0 |
7 |
7 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
28 |
|
| К Ф М Л Г Киров |
0 |
3 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
5 |
28 |
|
| 1 7 9 Д |
2 |
3 |
6 |
0 |
-1 |
5 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
5 |
27 |
|
| 1 5 1 1 Г |
4 |
4 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
26 |
|
| Ш Ц П М В |
0 |
0 |
6 |
0 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
5 |
24 |
|
| 1 3 6 3 В |
0 |
0 |
6 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
1 |
21 |
|
| Ш Ц П М Г |
0 |
0 |
6 |
0 |
0 |
7 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
21 |
|
| 2 0 1 А |
0 |
0 |
0 |
0 |
1 |
7 |
0 |
0 |
4 |
0 |
0 |
0 |
7 |
0 |
0 |
19 |
|
| 1 5 1 1 А |
0 |
6 |
6 |
0 |
0 |
3 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
2 |
17 |
|
| 1 7 1 Е |
0 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
13 |
|
| 2 9 3 А |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
13 |
|
| 1 5 8 0 Р |
4 |
0 |
6 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
12 |
|
| 6 5 4 Б |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
1 |
9 |
|