11 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите уравнение: 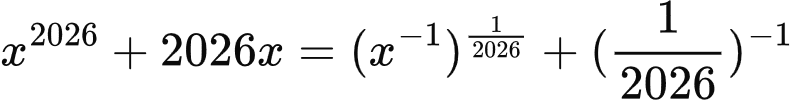 .
.
1.2. Пять квадратов расположены так, как показано на рисунке. Площади четырёх из них даны. Найдите площадь пятого, самого большого.
1.3. Найдите количество трёхзначных чисел, у которых сумма цифр равна 10.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Решите систему уравнений: 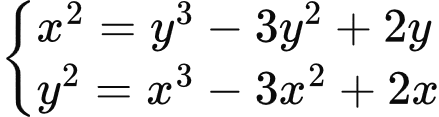 .
.
2.2. На высоте AH остроугольного треугольника ABC отмечена внутренняя точка X. Оказалось, что AB + СX = AC + ВX. Обязательно ли треугольник ABC – равнобедренный?
2.3. Пусть k – натуральное число. Известно, что среди 29 последовательных чисел 30k + 1, 30k + 2, . . ., 30k + 29 имеется 7 простых. Докажите, что первое и последнее из этих 29 чисел – простые.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют неравенству: x2 - (y + 1 / y)x + 1 > 0.
3.2. В правильной треугольной призме, каждое ребро которой равно 1, найдите расстояние между двумя отрезками: ребром основания и скрещивающейся с ним диагональю боковой грани.
3.3. Можно ли расставить числа 1, 2,..., 2025 по кругу так, чтобы из любой тройки подряд идущих чисел можно было составить арифметическую прогрессию?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Докажите, что tgα + tg(α + 20°) + tg(α + 40°) + ... + tg(α + 140°) + tg(α + 160°) = 9tg9α.
4.2. Точка, лежащая внутри равнобедренной трапеции, отношение оснований которой меньше чем 2 : 1, соединена отрезками со всеми вершинами. Докажите, что из этих четырёх отрезков можно сложить границу четырёхугольника, вписанного в эту трапецию (на каждой стороне трапеции лежит по одной вершине этого четырёхугольника).
4.3. Имеется n камней, которые можно разложить на две, три, четыре или пять кучек так, чтобы при каждом таком разбиении массы кучек были равны. При каком наименьшем n это возможно?
Пятый тур (15 минут; каждая задача – 7 баллов).