29 сентября 2002 года
Задания. Решения. Комментарии
МЦНМО
МОСКВА 2003
В скобках после номера задачи указаны классы, которым эта задача рекомендуется. Достаточно решить задачи своего класса, причём не обязательно все. Решать остальные задачи тоже можно.
1. (6-9) "Волшебный мостик". Перед вами две
фотографии деревянного мостика (через реку Белая, город Белорецк,
лето 2002 года). На левом фотоснимке видны перила с двух сторон мостика
(как это на самом деле и есть), а на правом - только с одной.
Куда и почему "делись" перила? (Перила никто не отпиливал,
фотомонтаж не применялся).
2. (6-9) Определите приблизительно среднюю скорость мячика во время игры в футбол.
3. (7-11) Трёхголовый Змей Горыныч нашёл в Чистом поле (никаких деревьев нет и вообще зацепиться не за что) кусок крепкой верёвки. Горыныч может каждой из своих голов вцепиться зубами в любое место верёвки и тянуть за это место в любую сторону с силой 1 Ньютон или меньше. Какую силу натяжения верёвка должна выдерживать, чтобы Змей Горыныч не смог её порвать? Неуклюжий Горыныч не может зацепить верёвку за себя и достать до неё лапами, крыльями или хвостом.
4. (8-9) Подвесим к штативу грузик на проволоке. Вынесем эту конструкцию на мороз. В результате охлаждения длина проволоки уменьшилась, грузик поднялся на некоторую высоту. Откуда взялась энергия для увеличения потенциальной энергии грузика?
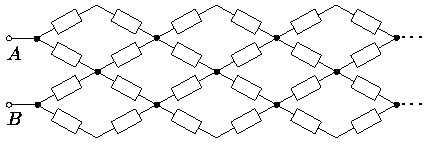
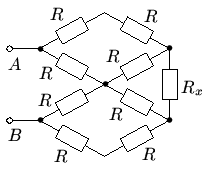
5. (8-11) Найти сопротивление между
точками A и B бесконечной цепочки резисторов
(сопротивление каждого резистора R).
6. (8-11) Иногда солнечный зайчик почти точно повторяет форму зеркала, которым его "пускают", иногда только приблизительно, а иногда солнечный зайчик по форме на зеркало совсем не похож. От чего это зависит?
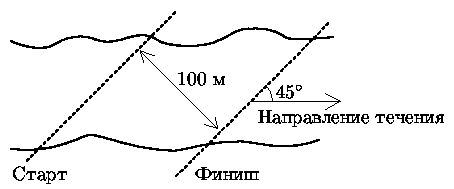
7. (9-11) Соревнования по плаванию проводятся
в речке со скоростью течения v0=5 км/ч. Линия финиша
натянута через речку под углом 45o к направлению течения.
Спортсмены размещаются выше по течению на расстоянии L=100 м от
линии финиша и после старта могут плыть в любом направлении. Через какое
время спортсмен, умеющий плавать со скоростью v, доплывёт до финиша,
если будет плыть в правильную сторону?
8. (10-11) Конец бревна привязали верёвкой длины h к якорю и эту конструкцию бросили в водоём. Построить график (или хотя бы эскиз графика) зависимости силы натяжения верёвки от уровня воды в водоёме. Плотность бревна r меньше плотности воды r0, длина бревна L, масса M. Верёвку можно считать нерастяжимой, тонкой и невесомой.
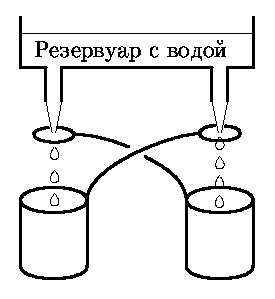
9. (10-11) "Устройство для получения электричества
из воды". Из резервуара с водой выходят две трубки,
из которых сквозь металлические кольца (расположенные около мест
образования капель) капает вода. Капли попадают в металлические сосуды,
каждый сосуд соединён проводом с кольцом, сквозь которое вода капает
в другой сосуд. Других электрических соединений в устройстве нет
(сосуды изолированы друг от друга и резервуара с водой).
В процессе капания воды металлические сосуды приобретают разноимённые
электрические заряды. Объясните, как и почему такое устройство работает.
1. Правый фотоснимок был сделан фотоаппаратом, установленным на горизонтальной поверхности левых перил моста. По ряду причин (разумеется, индивидуальных для каждого человека) эту поверхность (занимающую почти весь передний план фотоснимка) можно ошибочно принять за пешеходную поверхность моста.
Среди причин (ответ на вопрос "почему?") можно условно выделить
следующие:
1) фотография сделана в неестественном для человека ракурсе (расположить
глаза таким же образом, как фотоаппарат, трудно - мешается подбородок
и нос - если смотреть с конца перил);
2) весь мост изготовлен из одного и того же материала (дерева), длительное
время находившегося в сходных условиях (у поверхности воды, как понятно
из фотографии и условия задачи), поэтому все поверхности имеют одинаковые
оптические свойства (цвет, отражающая способность, светорассеяние) и
не различаются на фотографии по этим признакам;
3) граница тени на пешеходной поверхности от правых перил практически
совпадает с правой границей левых перил, из-за чего создаётся впечатление,
что эта тень падает не на "своё место", а на поверхность левых
перил, из-за чего эти поверхности путаются.
4) невысокое качество воспроизведения фотографии при тиражировании условий
задач на ризографе (заметим, что при рассматривании качественных цветных
оригиналов этих фотографий описанный в задаче зрительный эффект также
наблюдается).
При внимательном сравнении фотографий достаточно легко обнаружить, что на левом снимке пешеходная поверхность состоит примерно из 10 параллельных досок, а на правом - только из одной; причём размеры этой "доски" (ширина и длина) явно противоречат биологическим представлениям о высоте и диаметре растущих на земле деревьев.
2. Годятся любые разумные соображения. Например (из работы школьника, пересказ): "Во время игры мячик практически никогда не стоит на месте. За ним всё время бегают, но редко догоняют. Скорость бега человека примерно 3-4 м/с, значит средняя скорость мячика примерно 5 м/с".
Решения, авторы которых немного схитрили и рассматривали векторную среднюю скорость, также признавались правильными. Эта скорость, очевидно, примерно равна 0 и не больше, чем
(расстояние от центра до угла футбольного поля)/(время игры)
3. Ответ: 1 Ньютон.
Если верёвка выдерживает натяжение менее 1 Н, Змей Горыныч может порвать верёвку, растягивая её двумя головами.
Теперь докажем, что Горыныч не может натянуть какой-нибудь участок верёвки с силой больше 1 Н. Предположим, что Горынычу это каким-то образом удалось сделать. Уточним, что головой Змея Горыныча мы считаем точку, из которой может расходится несколько верёвок и модуль векторной суммы натяжений этих верёвок не больше 1 Ньютона.
Выберем участок верёвки, натянутый с силой больше 1 Ньютона (на рисунке показан жирным отрезком), и какую-нибудь точку на нём. Проведём через эту точку плоскость, перпендикулярную выбранному участку верёвки (пересечение этой плоскости с плоскостью рисунка показано пунктирной линией). Для простоты будем считать, что эта плоскость не проходит ни через какую голову (если это окажется не так - выберем другую точку и перпендикулярную плоскость, и т. д.; головы всего 3, поэтому на четвёртый раз нам обязательно повезёт).
С какой-то стороны от плоскости окажется не больше одной головы Горыныча (потому что у него всего 3 головы). И уравновесить силу натяжения выбранного участка верёвки с этой стороны от плоскости окажется невозможным. Получилось противоречие.
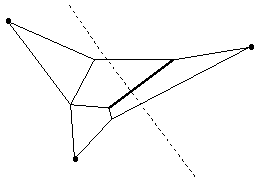
Приведённое выше решение (оно может показаться сложноватым) годится для случая, когда Змею Горынычу разрешается складывать верёвку, вязать узлы, делать "паутину", пропускать верёвку между зубами (по предложению участников турнира), используя их в качестве блоков, и т. п., то есть разбирается самый общий случай.
4. Основная работа по перемещению грузика на бо'льшую высоту была совершена проволокой. В тоже время внутренняя (тепловая) энергия проволоки в результате охлаждения уменьшилась. Логично предположить (так на самом деле и есть), что часть этой энергии пошла не на нагревание атмосферы, а на совершение работы по перемещению грузика.
Более тонкий (но существенный) эффект. Энергия упругой деформации проволоки (в простейшем случая равная (k(Dx)2)/2) в результате охлаждения могла уменьшиться (как в результате возможного уменьшения удлинения проволоки Dx, так и(или) в результате возможного уменьшения жёсткости k). В таком случае можно условно считать, что на увеличение потенциальной энергии грузика частично была потрачена энергия упругой деформации проволоки.
Один из участников турнира совершенно справедливо отметил, что внутренняя энергия проволоки сначала превращается в кинетическую (перемещение проволоки, кроме верхнего конца), а затем в потенциальную энергию грузика (в результате неупругого взаимодействия проволоки с грузиком).
Разумеется, приведённый список энергообменных процессов в рассматриваемой системе - не исчерпывающий. Например, можно учесть уменьшение потенциальной энергии атмосферы (направление силы Архимеда совпадает с направлением перемещения грузика). Этот эффект скорее всего окажется несущественным. Но формально в условии ничего не написано про массу и плотность грузика - каждый решающий задачу может представлять себе этот грузик по-своему.
5. Ответ: 21/2R.
Наиболее простой способ решения подобных задач с бесконечными цепочками - обозначить как-нибудь (например, Rx) сопротивление всей цепочки. Потом "отцепить" от цепочки часть так, чтобы оставшийся бесконечный "хвост" совпадал с исходной схемой. Затем заменить хвост на резистор сопротивлением Rx и рассчитать по обычным правилам сопротивление схемы из конечного числа резисторов (которое тоже равно Rx). Получится уравнение Rx=f(R, Rx), корнем (одним из корней) которого является решение задачи.
Приводим один из возможных вариантов реализации вышеописанной идеи решения для нашей задачи.
1. Обозначим сопротивление всей цепочки через Rx.
2. Оставим слева 8 резисторов, а оставшийся "хвост" (полностью совпадающий с исходной цепочкой) заменяем на резистор сопротивлением Rx.
3. Немного перерисуем схему, для удобства обозначим буквами C и D соединения в центральной части схемы.
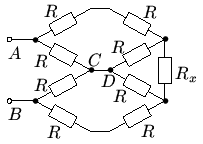
По проводу между точками C и D ток не течёт, поэтому этот провод из схемы можно удалить. (Пусть в направлении CD течёт ток I. Поменяем на клеммах A и B полярность на противоположную - с одной стороны ток должен измениться на -I, с другой - остаться таким же, так как получившаяся схема оказалась такой же, как и до перемены полярности. Следовательно, I=0. Другое пояснение. Получившаяся схема симметрична, и точка C, и точка D находятся на одной и той же "оси симметрии" и, следовательно, имеют одинаковые потенциалы. Если такие точки соединить проводом, ток по этому проводу не потечёт).
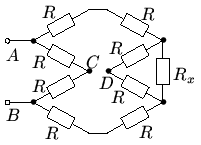
4. Заменяем все последовательные цепочки -R-R- на -2R-. Схема становится совсем простой.
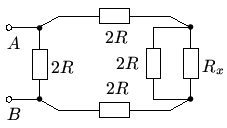5. Окончательно упрощаем схему
и сводим её к единственному резистору сопротивлением
| Rx | = | 2R*(((2R*Rx)/(2R+Rx)+4R) 2R+(((2R*Rx)/(2R+Rx)+4R) | = | 2R*((8R2+6R*Rx)/(2R+Rx)) 2R+((8R2+6R*Rx)/(2R+Rx)) |
6. Решаем полученное уравнение. Умножим числитель и знаменатель правой части уравнения на (2R+Rx)
| Rx | = | 2R*(8R2+6R*Rx) 2R*(2R+Rx)+8R2+6R*Rx |
Разделим числитель и знаменатель правой части уравнения на 2R
| Rx | = | 8R2+6R*Rx 2R+Rx+4R+3Rx |
| Rx | = | 8R2+6R*Rx 6R+4Rx |
| Rx | = | 4R2+4R*Rx 3R+2Rx |
Если R>0 (что часто подразумевается при употреблении термина "резистор"), то решение -21/2R не имеет физического смысла. Однако, бывают схемы и устройства, для которых формально выполняется закон Ома I=U/R, где величина R не является положительным числом. Отбор "лишних" корней в этом случае усложняется.
Бесконечные цепочки интересны не только сами по себе - они являются моделями многих явлений в электротехнике (например: два проводника - цепочки из резисторов с маленьким сопротивлением, изоляция между проводниками - поперечные резисторы с "большим" сопротивлением), биофизике (например, трубчатая нервная клетка, у которой сопротивление поверхностей мембраны существенно меньше сопротивления через мембрану) и др.
Мы очень подробно расписали решение задачи главным образом для тех читателей, которые столкнулись с бесконечными цепочками резисторов впервые - чтобы дать возможность хорошо во всём разобраться. От участников турнира такого подробного и длинного решения, разумеется, не требуется.
6. Предполагаем, что зеркало самое обыкновенное, в частности, плоское. Также для простоты будем считать плоской поверхность (экран), на которую падает "зайчик".
Первая очевидная причина возможного искажения формы зайчика - ориентация плоскости экрана (поверхности, на которой наблюдается изображение "зайчика"). Наклоняя экран под разными углами можно "растягивать" "зайчик" в разных направлениях.
Для упрощения объяснения будем временно считать солнечные лучи
параллельными и нарисуем схему образования "солнечного зайчика".
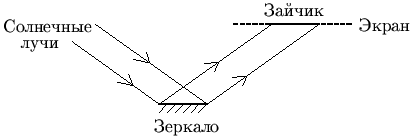
На этой схеме изображена ситуация, когда плоскость экрана параллельна плоскости зеркала (и обе они перпендикулярны плоскости страницы). Из простых геометрических соображений понятно, что форма зайчика в этом случае совпадает с формой зеркала.
А можно ли ещё как-нибудь расположить экран,
чтобы форма зайчика совпала с формой зеркала?
Построим на рисунке окружность, радиус которой равен длине отрезка,
изображающего "зайчик", а центром является левый конец этого
отрезка. Понятно, что есть ещё одна (и только одна, то есть всего
две для одного положения Солнца и зеркала)
такая ориентация плоскости экрана.
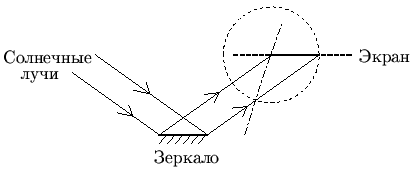
Эта ориентация показана штрихпунктирной линией - условной линией пересечения плоскости экрана (в этой ориентации) с плоскостью страницы (эти плоскости перпендикулярны).
Также понятно, что (при заданных положениях зеркала, Солнца и плоскости рисунка) если плоскость экрана не будет перпендикулярной плоскости рисунка, то зайчик растянется по экрану (в направлении, перпендикулярном линии пересечения плоскости экрана и плоскости рисунка).
Выше мы специально употребили слово "ориентация" вместо, например, слова "расположение", подчёркивая, что экран можно передвигать, но нельзя наклонять (менять ориентацию в пространстве).
Вторая причина - Солнце в условиях этой задачи нельзя считать точечным источником света, что очевидно, если (аккуратно!) на него посмотреть - Солнце видно с Земли в виде диска, а вовсе не точки. Солнечные лучи, следовательно, нельзя считать параллельными. В результате границы зайчика, которые в первом случае мы считали линиями, на самом деле оказываются размытыми. Ширина размытых границ может даже оказаться больше размеров зайчика (в этом случае "солнечный зайчик по форме на зеркало совсем не похож").
На каждую точку зеркала лучи попадают со всей видимой поверхности Cолнца
в виде конуса (угол при вершине этого конуса называется видимым угловым
размером Солнца и составляет примерно 0,5o) и отражаются
в виде конуса с таким же углом. На экране этот конус даст изображение в виде
окружности (или эллипса, если экран ориентирован не перпендикулярно
оси конуса). Легко сообразить, что любая деталь формы зеркала на изображении
"зайчика" будет "размазана" до размеров (диаметра)
такой окружности. Соответственно, все детали формы зеркала (в том
числе и его граница), по размерам намного бо'льшие диаметра этой окружности,
уцелеют, сравнимые с ней по размерам - окажутся размазанными,
а намного меньшие - станут незаметными [5 Эти детали
часто можно восстановить с помощью компьютерной обработки данных о форме
и распределении освещённости солнечного зайчика. "На глазок" это сделать
скорее всего невозможно, хотя у людей, длительное время занимающихся оптикой,
появляется определённый опыт оценки исходной формы предмета по размытому
изображению.].
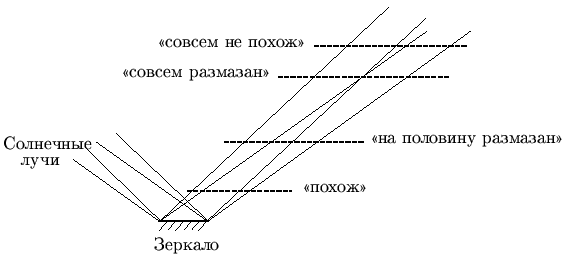
(на схеме угловые размеры Солнца для наглядности сильно преувеличены)
Очевидно, что если в центральной части зайчика касаются две окружности, образованные конусами от противоположных точек границы зеркала (это как раз соответствует пограничному случаю, когда контуры зайчика уже сильно размыты, но ещё повторяют контуры зеркала), то угол между направлениями на эти точки при наблюдении от зайчика как раз равен углу этих конусов (простое построение - вертикальные углы), то есть, в свою очередь, угловому размеру Солнца при наблюдении с Земли. Этот же угол вполне справедливо можно считать угловым размером зеркала при наблюдении от "зайчика".
Вывод: если угловые размеры зеркала существенно больше угловых размеров Солнца то форма границы зайчика достаточно точно повторяет контуры зеркала, если эти размеры примерно одинаковы - контуры зеркала воспроизводятся нечётко, если, наоборот, угловые размеры зеркала существенно меньше угловых размеров Солнца то форма контуров "зайчика" не зависит от формы зеркала [6 Но может случайно совпасть с формой зеркала, например, если зеркало - круглое и зайчик представляет собой размытое пятно округлой формы.]. (Имеются ввиду угловые размеры зеркала и Солнца при наблюдении с того места экрана, где расположено изображение "зайчика".)
Замечание. Если мы занимаемся пусканием Солнечных "зайчиков" не на Земле, а на другой планете, то в решении нужно заменить Землю на название этой планеты (угловые размеры Солнца при наблюдении с этой планеты будут другими, отличающимися от земных) [7 А Cолнце всегда останется на месте - в условии задачи сказано, что зайчик именно солнечный.].
7. Ответ: L/(v+v1) = L/(v+(v0/21/2)).
Пусть один из спортсменов плавать не умеет (только держится на воде, v=0). Тогда он доплывёт до финиша по течению, проплыв расстояние 21/2L за время t1=21/2L/v0. Его скорость сближения с линией финиша составляет v1=L/t=L/(21/2L/v0)=v0/21/2.
Другой спортсмен, стартовавший с того же места, умеющий плавать со скоростью v, может за время t уплыть от первого "спортсмена" на расстояние vt в любую сторону, в том числе и в сторону финиша.
Если к какому-то моменту времени t после старта расстояние от первого спортсмена до финиша равно vt, это как раз означает, что второй спортсмен в этот момент финишировал. Составим и решим уравнение.
vt = L-v1t
(v+v1)t = L
t = L/(v+v1) = L/(v+(v0/21/2))
8. Уровень воды в водоёме будем обозначать буквой H, силу натяжения верёвки - F.
Два участка графика строятся совсем просто. Если глубина меньше длины верёвки (H<h), то бревно будет свободно плавать на поверхности воды, верёвка при этом не натягивается (F=0).
Если глубина больше суммы длин верёвки и бревна (H>h+L), то бревно, очевидно, будет полностью находиться под водой. В этом случае на бревно действует сила Архимеда FАрх=r0gVбревна=(r0/r)Mg, которая уравновешивается силой тяжести Mg и силой натяжения верёвки F, то есть
F+Mg=(r0/r)Mg
и
F=FАрх-Mg=(r0/r)-Mg=((r0/r)-1)Mg
Теперь разберём промежуточный случай
h<H<h+L.
Возможное положение бревна в таком случае показано на рисунке
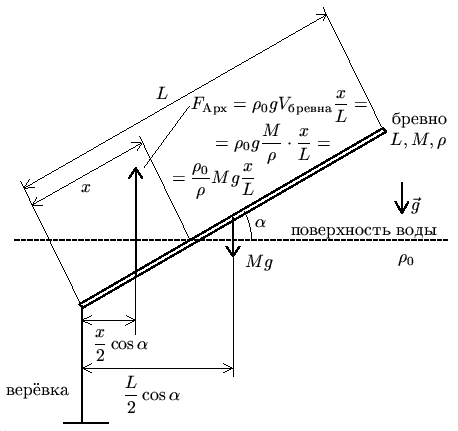
(вертикальность положения нити очевидна -
у силы тяжести и силы Архимеда, действующих на бревно, нет горизонтальных
составляющих, следовательно, эти силы не могут скомпенсировать горизонтальной
составляющей силы натяжения наклонной нити; условия устойчивости равновесия
бревна в вертикальном и наклонном положении в основном будут понятны
из дальнейшего решения, для простоты формально мы их определять не будем).
Пусть x - длина погруженной в воду части бревна, a - угол наклона бревна (угол между бревном и горизонталью). Сила Архимеда действует только на погруженную в воду часть бревна и она в x/L раз "больше" (меньше [8] Имеется ввиду, что силу нужно умножать на коэффициент x/L и x/L<1.) силы Архимеда, действующей на всё бревно, то есть равна (x/L)*(r0/r)Mg.
Чтобы бревно не вращалось в вертикальной плоскости вокруг конца, к которому привязана верёвка, необходимо равенство компенсирующих друг друга моментов силы тяжести и силы Архимеда относительно этого конца (других сил, действующих на бревно и имеющих ненулевые моменты относительно этой точки, нет).
Mg(L/2) cos a = (x/L)*(r0/r)Mg cos a
Сократим полученное уравнение (уравнение моментов) на очевидно не равное 0 выражение Mg/2, получится
L cos a = (x/L)*(r0/r) cos a
или
L2 cos a = x2(r0/r) cos a
Это условие может выполняться только или если cos a = 0 (то есть a = 90o - бревно находится в вертикальном положении и под водой может находится любая его часть), или
x=(r/r0)1/2L (угол a при этом может быть любым <90o, длина погруженной части бревна, как оказалось, не зависит от угла наклона).
В случае a<90o сила Архимеда, действующая на бревно (погруженный в воду участок бревна), равна
(x/L)*(r0/r)Mg = (((r/r0)1/2L)/L)(r0/r)Mg = (r0/r)1/2Mg ,
а сила натяжения верёвки (в этом случае), соответственно, разности силы Архимеда и силы тяжести
F = (r0/r)1/2Mg - Mg = ((r0/r)1/2-1)Mg
Теперь понятно, что после того, как уровень воды превысит значение h+(r/r0)1/2L, бревно примет вертикальное положение (любое другое положение противоречит уравнению моментов) и при дальнейшем увеличении уровня воды сила Архимеда и, следовательно, сила натяжения верёвки будут линейно возрастать до тех пор, пока бревно полностью не погрузится под воду; после этого силы меняться перестанут. Формулу для этой линейной зависимости можно легко получить, но, поскольку в условии задачи требуется только построить график, мы просто соединим две соответствующие точки на графике прямой линией.
Окончательный график получается таким:
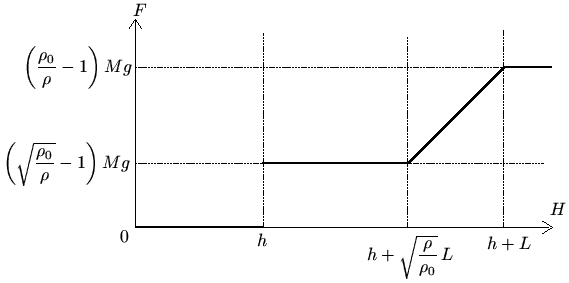
9. Сразу отметим, что устройство, собранное по приведённой в условии схеме, будет работать совсем не обязательно (к большому сожалению собирающих).
Кроме того, нереально придумать объяснение, подходящее ко всем работающим устройствам: для этого пришлось бы учесть все возможные детали конструкции каждого конкретного устройства и внешние условия, в которых оно находится.
Поэтому поступим так: сначала приведём простое, но очень поверхностное и неточное объяснение, а затем - наиболее интересные и не слишком сложные уточнения и разъяснения.
Простое объяснение. Пусть правая (на рисунке) банка и, соответственно, левое металлическое кольцо (соединённое с банкой проводником) имеют положительный электрический заряд, а левая банка и правое кольцо - отрицательный электрический заряд. (В том, как эти заряды возникли, мы пока разбираться не будем).
Вода - проводник, в ней находятся электрические заряды (положительные и отрицательные), которые могут перемещаться в пределах занимаемого водой объёма (но не могут этот объём покинуть, так как он ограничен изолирующими стенками сосуда и воздухом, который тоже плохо проводит электричество).
Под действием электростатических сил положительные заряды притягиваются к левому кольцу (и, соответственно, собираются в воде, находящейся около конца правой трубки), а отрицательные заряды по аналогичной причине располагаются около конца левой трубки. Явление перераспределения зарядов в проводнике в результате взаимодействия с другими заряженными телами называется поляризацией.
В результате капли воды, капающие из правой трубки, оказываются заряженными положительно, а капающие из левой трубки - заряженными отрицательно.
Капающие из правой трубки положительно заряженные капли пролетают сквозь отрицательно заряженное кольцо и затем попадают в положительно заряженную банку (силы притяжения капли к противоположно заряженному кольцу и отталкивания от одноимённо заряженной банки преодолеваются силой тяжести).
Аналогично, отрицательно заряженные капли, капающие из левой трубки, попадают в левую (отрицательно заряженную) банку.
Таким образом, в указанном процессе происходит накопление зарядов в металлических банках (и связанных с ними проводниками кольцах). По мере увеличения этих зарядов происходит усиление поляризации воды в резервуаре, и, вследствие этого, увеличение зарядов вновь образующихся капель (по сравнению с зарядами образовавшихся ранее). То есть процесс оказывается самонарастающим (или, по крайней мере, самоподдерживающимся).
Уточнения и разъяснения.
1. Объясняя причины перераспределения зарядов по находящейся в резервуаре воде, правильнее говорить об электростатических потенциалах, создаваемых в соответствующих местах (точнее, разности потенциалов между концом левой трубки и концом правой трубки). Когда на банках (а также кольцах и соединяющих их проводниках) уже накоплены достаточно большие заряды, именно эти заряды и вносят основной вклад в соответствующие потенциалы.
2. До этого момента основной вклад в потенциалы создают другие заряды, появление которых в каждом конкретном случае обусловлено случайными причинами (которые физики называют флуктуациями). Разность потенциалов может быть обусловлена потенциалом Земли, зарядами на одежде экспериментатора и зрителей, работой находящейся рядом радиоэлектронной аппаратуры, летающими по воздуху заряженными пылинками и т. п.
3. На первый взгляд может показаться странным, что в процессе работы "симметричного" устройства на одной из его "симметричных" частей появляется положительный заряд, а на другой - отрицательный. (Кто "решает", куда заряд какого знака поместить?)
Как уже объяснялось выше, это "решение" зависит от многих случайных причин. К тому же практически сделать абсолютно симметричную конструкцию невозможно. А если бы это и получилось - создать абсолютно симметричные внешние условия всё равно нельзя.
4. Как отмечалось и объяснялось выше, возникшее небольшое перераспределение зарядов может самопроизвольно нарастать. Но мы не утверждаем, что так будет всегда и обязательно. Прежде чем прибор "заработает", распределение зарядов может поменяться на противоположное, и не один раз.
5. Во всяком физическом эксперименте интересно не только теоретическое обоснование, но и результаты. То есть интересно проверить, действительно ли на банках и соединённых с ними металлических частях устройства скапливаются электрические заряды. Мы рекомендуем для этой цели несколько простых способов.
а) Подвесить на тоненькой проволочке к металлической части (заряд которой мы хотим проверить) два лёгких кусочка металлической фольги ("лепестка"), например, сделанных из обёртки конфеты. Когда накопится достаточно большой заряд, эти лепестки будут отталкиваться друг от друга. Лепестки должны висеть на проволоке свободно, например, в них можно проткнуть дырки и на проволоку надеть. Годится также кусочек новогоднего "дождика", который можно проткнуть посередине (лепестками будут два свисающих конца).
б) Соединить металлические банки проволокой, затем проволоку разрезать, оставив между разрезанными частями зазор не больше 1 мм. В темноте можно увидеть, как через этот зазор время от времени проскакивают искры.
в) Внимательно наблюдать за каплями. Их траектории в результате действия сил притяжения к кольцам и сил отталкивания от банок могут заметно искривляться.
г) Соединить металлические банки неоновой (газоразрядной лампочкой) - она будет периодически вспыхивать. Заметим, что нужна именно газоразрядная лампочка, которая "загорается" только при определённом напряжении, а до этого является изолятором. Обычная лампочка накаливания не годится - она является проводником и не даст накапливаться разноимённым зарядам. Аналогичная проблема может возникнуть и с электроизмерительными приборами (например, обычным школьным вольтметром).
В любом случае при проведении эксперимента требуется терпение - иногда заметный эффект не появляется достаточно долго - минут 5-10 или даже дольше. Почему это происходит? Одна из правдоподобных гипотез - на заряжающиеся части устройства оседают летающие вокруг пылинки противоположного знака (тем самым уменьшают заряд). Соответственно, приходится ждать, пока устройство "отловит" летающую вокруг заряженную пыль.
Описанное в задаче приспособление иногда называется "капельницей Кельвина", по имени предполагаемого изобретателя. Несколько усложнив конструкцию, на основе предложенной в условии задачи схемы можно собрать устройство, создающее напряжение в несколько тысяч Вольт; такие устройства раньше использовались в физических экспериментах в качестве простых (но не очень совершенных) генераторов высокого напряжения. Более подробное описание мы не даём - оно достаточно сложное для "школьной" книжки, и к тому же последствия экспериментов с высоким напряжением могут оказаться вредными для здоровья.
За каждую задачу ставилась одна из таких оценок:
+! + +. +- +/2 -+ -. - 0
Это традиционная система оценок для московских математических олимпиад
(см. пояснение на стр. 12).
Грамота "за успешное выступление на конкурсе по физике"
присуждалась за следующие (или лучшие) результаты.
1. В любом классе за хотя бы + за любую из задач N 6, 8, 9.
2. В классе не старше 10 за хотя бы + за любую из задач N 5, 7.
3. В классе не старше 8 за + за любую задачу.
4. В 9 классе за оценки + за любые две задачи.
5. В 9 классе за одну оценку + и две оценки +/2 за любые задачи.
6. В классах 10 и 11 за оценку + кроме задач N 1 и N 2 и ещё один +.
7. В классах 10 и 11 за оценку + кроме задач N 1 и N 2 и ещё три оценки +/2 (за любые задачи).
Участникам, не получившим грамоту, балл многоборья присуждался
за следующие (или лучшие) результаты.
1. В классе не старше 6 за оценку +/2 за любую задачу.
2. В классах 7 и 8 - за оценки +/2 за любые две задачи.
3. В классах 9 и 10 - за оценки +/2 за любые три задачи.
4. В 11 классе - за оценки +/2 за любые четыре задачи.